Question

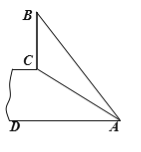
【題目】如圖，斜坡AC的坡度（坡比）為1: ，AC＝10米．坡頂有一垂直于水平面的旗桿BC，旗桿頂端B點與A點有一條彩帶AB相連，AB＝14米．試求旗桿BC的高度．

Answer 1

【答案】6米.

【解析】

試題分析：如果延長BC交AD于E點，則CE⊥AD，要求BC的高度，就要知道BE和CE的高度，就要先求出AE的長度．直角三角形ACE中有坡比，由AC的長，那么就可求出AE的長，然后求出BE、CE的高度，BC=BE-CE，即可得出結果．

試題解析：延長BC交AD于E點，則CE⊥AD．

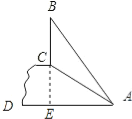
在Rt△AEC中，AC=10，由坡比為1：可知：∠CAE=30°，

∴CE=ACsin30°=10×=5，

AE=ACcos30°=10×=5．

在Rt△ABE中，．

∵BE=BC+CE，

∴BC=BE-CE=11-5=6（米）．

答：旗桿的高度為6米.

考點: 解直角三角形的應用-坡度坡角問題．