【題目】某電器商店計劃從廠家購進
兩種不同型號的電風扇，若購進8臺
型和20臺
型電風扇，需資金7600元，若購進4臺型和15臺型電風扇，需資金5300元.
（1）求型電風扇每臺的進價各是多少元；
（2）該商店經理計劃進這兩種電風扇共50臺，而可用于購買這兩種電風扇的資金不超過12800元，根據市場調研，銷售一臺型電風扇可獲利80元，銷售一臺型電風扇可獲利120元.若兩種電扇銷售完時，所獲得的利潤不少于5000元.問有哪幾種進貨方案？哪種方案獲得最大？最大利潤是多少？
【答案】（1）
型電風扇每臺進價分別為200元、300元.；（2）當
即方案一獲利最大，最大利潤是5120元.
【解析】
（1）設
型電風扇每臺的進價分別為
元、
元，根據條件“若購進8臺
型和20臺
型電風扇，需資金7600元，若購進4臺型和15臺型電風扇，需資金5300元 ” 可列出關于x、y的二元一次方程組，解方程組即可得出結論；
(2) 設購進型電風扇
臺，則購進B型電風扇（50-a）臺，根據總價=單價×數量結合總利潤=單臺利潤×銷售數量，即可得出關于a的一元一次不等式組，解之即可得出a的取值范圍，取其內的整數即可找出各購買方案，再求出各方案獲得的利潤，比較后即可得出結論．
（1）設型電風扇每臺的進價分別為元、元
根據題意得
解得
所以型電風扇每臺進價分別為200元、300元.
（2）設購進型電風扇臺，
由題意得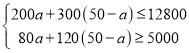
解得
，
∴共有4種進貨方案：
方案一：型
型
方案二： 23 27
方案三： 24 26
方案四 25 25
獲利：
∵
隨的增大而減小，
∴當即方案一獲利最大，最大利潤是5120元.
教學練新同步練習系列答案
課前課后同步練習系列答案
課堂小作業系列答案
黃岡小狀元口算速算練習冊系列答案
成功訓練計劃系列答案科目：初中數學 來源： 題型：
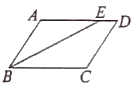
【題目】如圖已知BE平分∠ABC，E點在線段AD上，∠ABE＝∠AEB，AD與BC平行嗎？為什么？
解：因為BE平分∠ABC（已知）
所以∠ABE＝∠EBC （ ）
因為∠ABE＝∠AEB（ ）
所以∠ ＝∠ （ ）
所以AD∥BC （ ）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，點
的坐標為(0，4)，線段
的位置如圖所示，其中點
的坐標為(
，
)，點
的坐標為(3，
).
(1)將線段平移得到線段
，其中點的對應點為，點的對應點為點
.
①點平移到點的過程可以是：先向 平移 個單位長度，再向 平移 個單位長度；
②點的坐標為 .
(2)在(1)的條件下，若點
的坐標為(4，0)，連接
，畫出圖形并求
的面積.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，四邊形ABCD四條邊上的中點分別為E、F、G、H，順次連接EF、FG、GH、HE，得到四邊形EFGH（即四邊形ABCD的中點四邊形）.
（1）四邊形EFGH的形狀是 _____________ ，（證明你的結論. ）
（2）當四邊形ABCD的對角線滿足 __________條件時，四邊形EFGH是矩形(不用證明)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知矩形ABCD中，E是AD邊上的一個動點，點F，G，H分別是BC，BE，CE的中點．
（1）求證：△BGF≌△FHC；
（2）設AD=a，當四邊形EGFH是正方形時，求矩形ABCD的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，在等邊三角形ABC中，BC＝8cm，射線AG∥BC，點E從點A出發沿射線AG以1cm/s的速度運動，同時點F從點B出發沿射線BC以2cm/s的速度運動，設運動時間為t（s）．
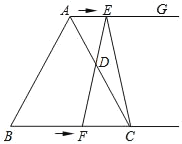
（1）連接EF，當EF經過AC邊的中點D時，求證：四邊形AFCE是平行四邊形；
（2）填空：①當t為 s時，四邊形ACFE是菱形；②當t為 s時，△ACE的面積是△ACF的面積的2倍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了解學生整體的數學學習能力，年級組織了“數學鉆石活動”，從中隨機抽取部分學生的成績進行統計分析，整理得到如下不完整的頻數分布表和數分布直方圖：
(1)表中的
，
；
(2)把上面的頻數分布直方圖補充完整；
(3)根據調查結果，估計年級500名學生中，成績不低于85分的人數。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將正方形 ABCD 繞點 A 按逆時針方向旋轉到正方形AB ' C ' D ' ，旋轉角為 （ 0＜＜ 180 ） ，連接 B ' D 、 C ' D ，若 B ' D C ' D ，則 =____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】探究與發現：
如圖1所示的圖形，像我們常見的學習用品--圓規．我們不妨把這種圖形叫做“規形圖”，那么在這一個簡單的圖形中，到底隱藏了哪些數學知識呢？請解決以下問題：
(1)觀察“規形圖”，試探究∠BPC與∠A、∠B、∠C之間的關系，并說明理由；
(2)請你直接利用以上結論，解決以下問題：
①如圖2：已知△ABC，BP平分∠ABC，CP平分∠ACB，直接寫出∠BPC與∠A之間存在的等量關系為： ．
遷移運用：如圖3：在△ABC中，∠A=80°，點O是∠ABC，∠ACB角平分線的交點，點P是∠BOC，∠OCB角平分線的交點，若∠OPC=100°，則∠ACB的度數 ．
②如圖4：若D點是△ABC內任意一點，BP平分∠ABD，CP平分∠ACD．直接寫出∠BDC、∠BPC、∠A之間存在的等量關系為 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com