
【題目】如圖,對稱軸為直線![]() 的拋物線
的拋物線![]() 與x軸相交于A、B兩點,其中A點的坐標為(-3,0)。
與x軸相交于A、B兩點,其中A點的坐標為(-3,0)。

(1)求點B的坐標;
(2)已知![]() ,C為拋物線與y軸的交點。
,C為拋物線與y軸的交點。
①若點P在拋物線上,且![]() ,求點P的坐標;
,求點P的坐標;
②設點Q是線段AC上的動點,作QD⊥x軸交拋物線于點D,求線段QD長度的最大值。
【答案】解:(1)∵A、B兩點關于對稱軸![]() 對稱 ,且A點的坐標為(-3,0),
對稱 ,且A點的坐標為(-3,0),
∴點B的坐標為(1,0)。
(2)①∵拋物線![]() ,對稱軸為
,對稱軸為![]() ,經過點A(-3,0),
,經過點A(-3,0),
∴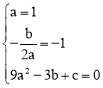 ,解得
,解得![]() 。
。
∴拋物線的解析式為![]() 。
。
∴B點的坐標為(0,-3)。∴OB=1,OC=3。∴![]() 。
。
設點P的坐標為![]() ,則
,則![]() 。
。
∵![]() ,∴
,∴![]() ,解得
,解得![]() 。
。
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
∴點P的坐標為(2,5)或(-2,-3)。
②設直線AC的解析式為![]() ,將點A,C的坐標代入,得:
,將點A,C的坐標代入,得:
![]() ,解得:
,解得:![]() 。
。
∴直線AC的解析式為![]() 。
。
∵點Q在線段AC上,∴設點Q的坐標為![]() 。
。
又∵QD⊥x軸交拋物線于點D,∴點D的坐標為![]() 。
。
∴![]() 。
。
∵![]() ,∴線段QD長度的最大值為
,∴線段QD長度的最大值為![]() 。
。
【解析】(1)由拋物線的對稱性直接得點B的坐標。
(2)①用待定系數法求出拋物線的解析式,從而可得點C的坐標,得到![]() ,設出點P 的坐標,根據
,設出點P 的坐標,根據![]() 列式求解即可求得點P的坐標。
列式求解即可求得點P的坐標。
②用待定系數法求出直線AC的解析式,由點Q在線段AC上,可設點Q的坐標為![]() ,從而由QD⊥x軸交拋物線于點D,得點D的坐標為
,從而由QD⊥x軸交拋物線于點D,得點D的坐標為![]() ,從而線段QD等于兩點縱坐標之差,列出函數關系式應用二次函數最值原理求解。
,從而線段QD等于兩點縱坐標之差,列出函數關系式應用二次函數最值原理求解。


 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC,∠C=90°,AC=12,BC=6,一條線段PQ=AB,P、Q兩點分別在AC和過點A且垂直于AC的射線AX上運動,要使△ABC和△QPA全等,則AP= ______ .

查看答案和解析>>
科目:初中數學 來源: 題型:
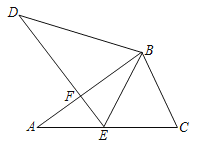
【題目】如圖,已知∠A=∠D,AB=DB,點E在AC邊上,∠AED=∠CBE,AB和DE相交于點F.
(1)求證:△ABC≌△DBE.
(2)若∠CBE=50°,求∠BED的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
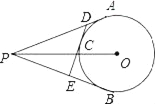
【題目】如圖,PA、PB切⊙O于A、B,點C在弧AB上,DE切⊙O于C,交PA、PB于D、E,已知PO=13cm,⊙O的半徑為5cm,則△PDE的周長是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了落實黨的“精準扶貧”政策,A、B兩城決定向C、D兩鄉運送肥料以支持農村生產,已知A、B兩城共有肥料500噸,其中A城肥料比B城少100噸,從A城往C、D兩鄉運肥料的費用分別為20元/噸和25元/噸;從B城往C、D兩鄉運肥料的費用分別為15元/噸和24元/噸.現C鄉需要肥料240噸,D鄉需要肥料260噸.
(1)A城和B城各有多少噸肥料?
(2)設從A城運往C鄉肥料x噸,總運費為y元,求出最少總運費.
(3)由于更換車型,使A城運往C鄉的運費每噸減少a(0<a<6)元,這時怎樣調運才能使總運費最少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】古埃及人用下面的方法得到直角三角形,把一根長繩打上等距離的13個結(12段),然后用樁釘釘成一個三角形,如圖1,其中∠C便是直角.
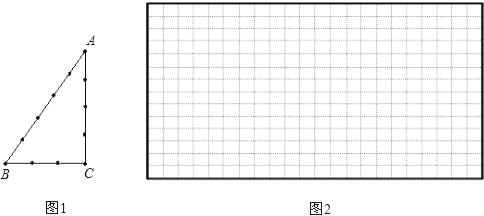
(1)請你選擇古埃及人得到直角三角形這種方法的理由 (填A或B)
A.勾股定理:在直角三角形邊的兩直角邊的平方和等于斜邊的平方
B.勾股定理逆定理:如果三角形的三邊長a、b、c有關系:a2+b2=c2,那么這個三角形是直角三角形
(2)如果三個正整數a、b、c滿足a2+b2=c2,那么我們就稱 a、b、c是一組勾股數,請你寫出一組勾股數
(3)仿照上面的方法,再結合上面你寫出的勾股數,你能否只用繩子,設計一種不同于上面的方法得到一個直角三角形(在圖2中,只需畫出示意圖.)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一個晾衣架放置在水平地面上,在其示意圖中,支架OA、OB的長均為100cm,支架OA與水平晾衣架OC的夾角∠AOC為59°,則支架兩個著地點之間的距離AB為_____cm.
(參考數據:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)

查看答案和解析>>
科目:初中數學 來源: 題型:
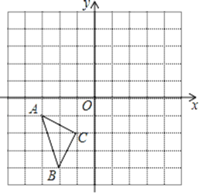
【題目】在如圖所示的直角坐標系中,每個小方格都是邊長為1的正方形,△ABC的頂點均在格點上,點A的坐標是(﹣3,﹣1).
(1)將△ABC沿y軸正方向平移3個單位得到△A1B1C1,畫出△A1B1C1,并寫出點B1的坐標;
(2)畫出△A1B1C1關于y軸對稱的△A2B2C2,并寫出點C2的坐標;
(3)求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
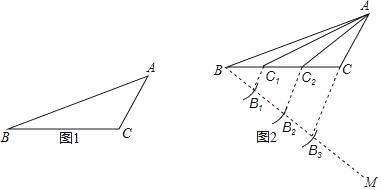
【題目】石景山區八角北路有一塊三角形空地(如圖1)準備綠化,擬從點A出發,將△ABC分成面積相等的三個三角形,栽種三種不同的花草.
下面是小美的設計(如圖2).
作法:(1)作射線BM;
(2)在射線BM上順次截取BB1=B1B2=B2B3;
(3)連接B3C,分別過B1、B2作B1C1∥B2C2∥B3C,交BC于點C1、C2;
(4)連接AC1、AC2.則![]() .
.
請回答,![]() 成立的理由是:
成立的理由是:
①_____;
②_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com