
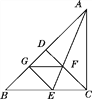
【題目】如圖,在△ABC中,∠ACB=90°,CD是AB邊上的高,∠BAC的平分線AE交CD于點F,交BC于點E,過點E作EG⊥AB于G,連結GF.求證:四邊形CFGE是菱形.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點A的坐標為(-2,3),點B的坐標為(-2,-3),那么點A和點B的位置關系是( )
A. 關于x軸對稱 B. 關于y軸對稱
C. 關于原點對稱 D. 關于坐標軸和原點都不對稱
查看答案和解析>>
科目:初中數學 來源: 題型:
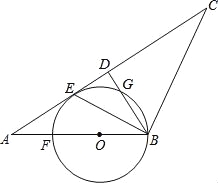
【題目】如圖,在△ABC中,AB=BC,D是AC中點,BE平分∠ABD交AC于點E,點O是AB上一點,⊙O過B、E兩點,交BD于點G,交AB于點F.
(1)判斷直線AC與⊙O的位置關系,并說明理由;
(2)當BD=6,AB=10時,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
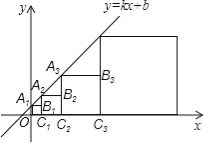
【題目】在直角坐標系中,正方形A1B1C1O1、A2B2C2C1、…、AnBnCnCn﹣1按如圖所示的方式放置,其中點A1、A2、A3、…、An均在一次函數y=kx+b的圖象上,點C1、C2、C3、…、Cn均在x軸上.若點B1的坐標為(1,1),點B2的坐標為(3,2),則點An的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在□ABCD中,AC、BD交于點O,過點O作直線EF、GH,分別交平行四邊形的四條邊于E、G、F、H四點,連接EG、GF、FH、HE.
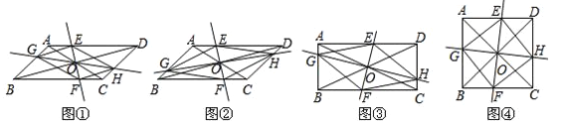
(1)如圖①,試判斷四邊形EGFH的形狀,并說明理由;
(2)如圖②,當EF⊥GH時,四邊形EGFH的形狀是 ;
(3)如圖③,在(2)的條件下,若AC=BD,四邊形EGFH的形狀是 ;
(4)如圖④,在(3)的條件下,若AC⊥BD,試判斷四邊形EGFH的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
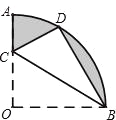
【題目】如圖,在扇形OAB中,∠AOB=90°,半徑OA=6.將扇形OAB沿過點B的直線折疊,點O恰好落在弧AB上點D處,折痕交OA于點C,則有下列選項:
①∠ACD=60°;
②CB=6![]() ;
;
③陰影部分的周長為12+3π;
④陰影部分的面積為9π﹣12![]() .
.
其中正確的是 (填寫編號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com