
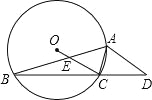
【題目】如圖所示,⊙O的內接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延長線于D點,OC交AB于E點.
(1)求∠D的度數;
(2)求證:AC2=ADCE.
【答案】(1)45°
(2)證明見解析
【解析】
試題分析: (1)連接OA,由圓周角∠ABC與圓心角∠AOC所對的弧為同一條弧,根據同弧所對的圓心角等于所對圓周角的2倍,由∠ABC的度數求出∠AOC的度數,再由OA=OC,根據等邊對等角,由頂角∠AOC的度數,利用三角形的內角和定理求出底角∠ACO的度數,再由∠BAC及∠ABC的度數,求出∠ACB的度數,由∠ACB﹣∠ACO求出∠BCE的度數,由OC與AD平行,根據兩直線平行同位角相等可得∠D=∠BCE,可得出∠D的度數;
(2)由∠ACB的度數,利用鄰補角定義求出∠ACD的度數,再由∠AEC為三角形BEC的外角,利用外角性質得到∠AEC=∠ABC+∠BCE,可得出∠AEC的度數,進而得到∠AEC=∠ACD,在三角形ACD中,由∠ACD及∠D的度數,求出∠CAD的度數,可得∠CAD=∠ACE,利用兩對對應角相等的三角形相似可得三角形AEC與三角形DCA相似,根據相似三角形的對應邊成比例可得證.
解:(1)連接OA,如圖所示:

∵圓周角∠ABC與圓心角∠AOC所對的弧都為![]() ,
,
∴∠AOC=2∠ABC,又∠ABC=15°,
∴∠AOC=30°,
又OA=OC,∴∠OAC=∠OCA=![]() =75°,
=75°,
又∠BAC=45°,∠ABC=15°,
∴∠ACB=120°,
∴∠OCB=∠ACB﹣∠ACO=120°﹣75°=45°,
又OC∥AD,
∴∠D=∠OCB=45°;
(2)∵∠ABC=15°,∠OCB=45°,
∴∠AEC=60°,
又∠ACB=120°∴∠ACD=60°,
∴∠AEC=∠ACD=60°,
∵∠D=45°,∠ACD=60°,
∴∠CAD=75°,又∠OCA=75°,
∴∠CAD=∠OCA=75°,
∴△ACE∽△DAC,
∴![]() =
=![]() ,即AC2=ADCE.
,即AC2=ADCE.


科目:初中數學 來源: 題型:
【題目】直線AB∥CD,EF分別交AB、CD于點M、N,NP平分∠MND. 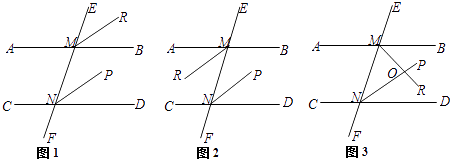
(1)如圖1,若MR平分∠EMB,則MR∥NP.請你把下面的解答過程補充完整: 解:因為AB∥CD(已知)
所以∠EMB=∠END()
因為MR平分∠EMB,NP平分∠MND(已知)
所以∠EMR= ![]() ∠EMB,∠MNP=
∠EMB,∠MNP= ![]() ∠MND(角平分線定義)
∠MND(角平分線定義)
所以∠EMR=∠MNP
所以MR∥NP()
(2)如圖2,若MR平分∠AMN,則MR與NP又怎樣的位置關系?請在橫線上寫出你的猜想結論:;
(3)如圖3,若MR平分∠BMN,則MR與NP又怎樣的位置關系?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
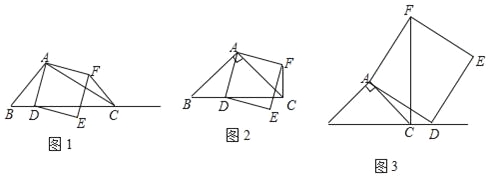
【題目】如圖1,在△ABC中,∠ACB為銳角,點D為射線BC上一點,聯結AD,以AD為一邊且在AD的右側作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①當點D在線段BC上時(與點B不重合),如圖2,將△ABD繞A點逆時針旋轉90°,所得到的三角形為 ,線段CF、BD所在直線的位置關系為 ,線段CF、BD的數量關系為 ;
②當點D在線段BC的延長線上時,如圖3,①中的結論是否仍然成立,并說明理由;
(2)如果AB≠AC,∠BAC是銳角,點D在線段BC上,當∠ACB滿足什么條件時,CF⊥BC(點C、F不重合),并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】畫圖并填空:如圖,方格紙中每個小正方形的邊長都為1.在方格紙內將△ABC經過一次平移后得到△A′B′C′,圖中標出了點B的對應點B′.
(1)在給定方格紙中畫出平移后的△A′B′C′;畫出AB邊上的中線CD;畫出BC邊上的高線AE;
(2)△A′B′C′的面積為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com