
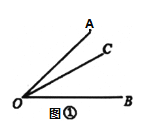
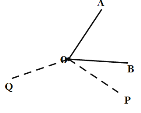
【題目】(理解新知)如圖①,已知![]() ,在
,在![]() 內(nèi)部畫(huà)射線
內(nèi)部畫(huà)射線![]() ,得到三個(gè)角,分別為
,得到三個(gè)角,分別為![]() ,
,![]() ,
,![]() ,若這三個(gè)角中有一個(gè)角是另外一個(gè)角的兩倍,則稱(chēng)射線
,若這三個(gè)角中有一個(gè)角是另外一個(gè)角的兩倍,則稱(chēng)射線![]() 為
為![]() 的“二倍角線”.
的“二倍角線”.
(1)一個(gè)角的角平分線______這個(gè)角的“二倍角線”(填“是”或“不是”)
(2)若![]() ,射線
,射線![]() 為
為![]() 的“二倍角線”,則
的“二倍角線”,則![]() 的大小是______;
的大小是______;
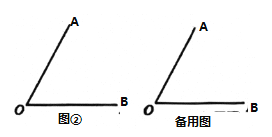
(解決問(wèn)題)如圖②,己知![]() ,射線
,射線![]() 從
從![]() 出發(fā),以
出發(fā),以![]() /秒的速度繞
/秒的速度繞![]() 點(diǎn)逆時(shí)針旋轉(zhuǎn);射線
點(diǎn)逆時(shí)針旋轉(zhuǎn);射線![]() 從
從![]() 出發(fā),以
出發(fā),以![]() /秒的速度繞
/秒的速度繞![]() 點(diǎn)順時(shí)針旋轉(zhuǎn),射線
點(diǎn)順時(shí)針旋轉(zhuǎn),射線![]() ,
,![]() 同時(shí)出發(fā),當(dāng)其中一條射線回到出發(fā)位置的時(shí)候,整個(gè)運(yùn)動(dòng)隨之停止,設(shè)運(yùn)動(dòng)的時(shí)間為
同時(shí)出發(fā),當(dāng)其中一條射線回到出發(fā)位置的時(shí)候,整個(gè)運(yùn)動(dòng)隨之停止,設(shè)運(yùn)動(dòng)的時(shí)間為![]() 秒.
秒.
(3)當(dāng)射線![]() ,
,![]() 旋轉(zhuǎn)到同一條直線上時(shí),求
旋轉(zhuǎn)到同一條直線上時(shí),求![]() 的值;
的值;
(4)若![]() ,
,![]() ,
,![]() 三條射線中,一條射線恰好是以另外兩條射線為邊組成的角的“二倍角線”,直接寫(xiě)出
三條射線中,一條射線恰好是以另外兩條射線為邊組成的角的“二倍角線”,直接寫(xiě)出![]() 所有可能的值______.
所有可能的值______.
【答案】(1)是;(2)![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() ;(4)
;(4)![]() 或
或![]() .
.
【解析】
(1)若OC為![]() 的角平分線,由角平分線的定義可得
的角平分線,由角平分線的定義可得![]() ,由二倍角線的定義可知結(jié)論;
,由二倍角線的定義可知結(jié)論;
(2)根據(jù)二倍角線的定義分![]() 三種情況求出
三種情況求出![]() 的大小即可.
的大小即可.
(3)當(dāng)射線![]() ,
,![]() 旋轉(zhuǎn)到同一條直線上時(shí),
旋轉(zhuǎn)到同一條直線上時(shí),![]() ,即
,即![]() 或
或![]() ,或OP和OQ重合時(shí),即
,或OP和OQ重合時(shí),即![]() ,用含t的式子表示出OP、OQ旋轉(zhuǎn)的角度代入以上三種情況求解即可;
,用含t的式子表示出OP、OQ旋轉(zhuǎn)的角度代入以上三種情況求解即可;
(4)結(jié)合“二倍角線”的定義,根據(jù)t的取值范圍分![]() ,
,![]() ,
,![]() ,
,![]() 4種情況討論即可.
4種情況討論即可.
解:(1)若OC為![]() 的角平分線,由角平分線的定義可得
的角平分線,由角平分線的定義可得![]() ,由二倍角線的定義可知一個(gè)角的角平分線是這個(gè)角的“二倍角線”;
,由二倍角線的定義可知一個(gè)角的角平分線是這個(gè)角的“二倍角線”;
(2)當(dāng)射線![]() 為
為![]() 的“二倍角線”時(shí),有3種情況,
的“二倍角線”時(shí),有3種情況,
①![]() ,
,![]() ;
;
②![]() ,
,![]() ,
,![]() ,
,![]() ;
;
③![]() ,
,![]() ,
,![]() ,
,
綜合上述,![]() 的大小為
的大小為![]() 或
或![]() 或
或![]() ;
;
(3)當(dāng)射線![]() ,
,![]() 旋轉(zhuǎn)到同一條直線上時(shí),有以下3種情況,
旋轉(zhuǎn)到同一條直線上時(shí),有以下3種情況,
①如圖
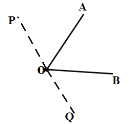
此時(shí)![]() ,即
,即![]() ,解得
,解得![]() ;
;
②如圖
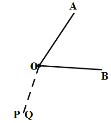
此時(shí)點(diǎn)P和點(diǎn)Q重合,可得![]() ,即
,即![]() ,解得
,解得![]() ;
;
③如圖
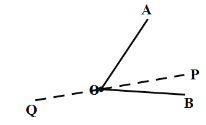
此時(shí)![]() ,即
,即![]() ,解得
,解得![]() ,
,
綜合上述,![]() 或
或![]() 或
或![]() ;
;
(4)由題意運(yùn)動(dòng)停止時(shí)![]() ,所以
,所以![]() ,
,
①當(dāng)![]() 時(shí),如圖,
時(shí),如圖,
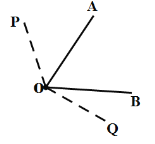
此時(shí)OA為![]() 的“二倍角線”,
的“二倍角線”,![]() ,
,
即![]() ,解得
,解得![]() ;
;
②當(dāng)![]() 時(shí),如圖,
時(shí),如圖,
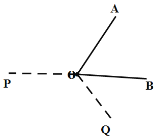
此時(shí),![]() ,所以不存在;
,所以不存在;
③當(dāng)![]() 時(shí),如圖
時(shí),如圖
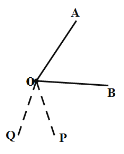
此時(shí)OP為![]() 的“二倍角線”,
的“二倍角線”,![]() ,
,
即![]()
解得 ![]() ;
;
④當(dāng)![]() 時(shí),如圖,
時(shí),如圖,
此時(shí)![]() ,所以不存在;
,所以不存在;
綜上所述,當(dāng)![]() 或
或![]() 時(shí),
時(shí),![]() ,
,![]() ,
,![]() 三條射線中,一條射線恰好是以另外兩條射線為邊組成的角的“二倍角線”.
三條射線中,一條射線恰好是以另外兩條射線為邊組成的角的“二倍角線”.


 階梯計(jì)算系列答案
階梯計(jì)算系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,為測(cè)量一座山峰CF的高度,將此山的某側(cè)山坡劃分為AB和BC兩段,每一段山坡近似是“直”的,測(cè)得坡長(zhǎng)AB=800米,BC=200米,斜坡AB的坡度![]() ,仰角∠CBE=50°.則山峰的高度CF約為( )米.(可用的參考數(shù)據(jù):sin50°≈0.8,tan50°≈1.2,
,仰角∠CBE=50°.則山峰的高度CF約為( )米.(可用的參考數(shù)據(jù):sin50°≈0.8,tan50°≈1.2, ![]() )
)
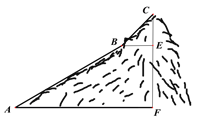
A. 500 B. 518 C. 530 D. 580
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某中學(xué)為了科學(xué)建設(shè)“學(xué)生健康成長(zhǎng)工程”.隨機(jī)抽取了部分學(xué)生家庭對(duì)其家長(zhǎng)進(jìn)行了主題為“周末孩子在家您關(guān)心嗎?”的問(wèn)卷調(diào)查,將回收的問(wèn)卷進(jìn)行分析整理,得到了如下的樣本統(tǒng)計(jì)表和扇形統(tǒng)計(jì)圖:
代號(hào) | 情況分類(lèi) | 家庭數(shù) |
| 帶孩子玩并且關(guān)心其作業(yè)完成情況 | 16 |
| 只關(guān)心其作業(yè)完成情況 | b |
| 只帶孩子玩 | 8 |
| 既不帶孩子玩也不關(guān)心其作業(yè)完成情況 | d |
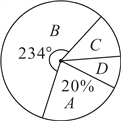
(1)求![]() 的值;
的值;
(2)該校學(xué)生家庭總數(shù)為500,學(xué)校決定按比例在![]() 類(lèi)家庭中抽取家長(zhǎng)組成培訓(xùn)班,其比例為
類(lèi)家庭中抽取家長(zhǎng)組成培訓(xùn)班,其比例為![]() 類(lèi)取20%,
類(lèi)取20%,![]() 類(lèi)各取60%,請(qǐng)你估計(jì)該培訓(xùn)班的家庭數(shù);
類(lèi)各取60%,請(qǐng)你估計(jì)該培訓(xùn)班的家庭數(shù);
(3)若在![]() 類(lèi)家庭中只有一個(gè)城鎮(zhèn)家庭,其余是農(nóng)村家庭,請(qǐng)用列舉法求出在
類(lèi)家庭中只有一個(gè)城鎮(zhèn)家庭,其余是農(nóng)村家庭,請(qǐng)用列舉法求出在![]() 類(lèi)中隨機(jī)抽出2個(gè)家庭進(jìn)行深度采訪,其中有一個(gè)是城鎮(zhèn)家庭的概率.
類(lèi)中隨機(jī)抽出2個(gè)家庭進(jìn)行深度采訪,其中有一個(gè)是城鎮(zhèn)家庭的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在一次數(shù)學(xué)課上,老師在屏幕上出示了一個(gè)例題:在△ABC中,D,E分別是AB,AC上的一點(diǎn),BE與CD交于點(diǎn)O,畫(huà)出圖形(如圖),給出下列四個(gè)條件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.
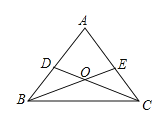
(1)要求同學(xué)從這四個(gè)等式中選出兩個(gè)作為已知條件,可判定△ABC是等腰三角形.
請(qǐng)你用序號(hào)在橫線上寫(xiě)出所有情形.答:
(2)選擇第(1)題中的一種情形,說(shuō)明△ABC是等腰三角形的理由,并寫(xiě)出解題過(guò)程.
解:我選擇 .
證明:
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
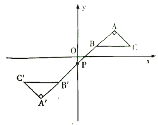
【題目】如圖,在平面直角坐標(biāo)系中,![]() 的頂點(diǎn)
的頂點(diǎn)![]() 在第一象限,點(diǎn)
在第一象限,點(diǎn)![]() 、
、![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() 、
、![]() ,
,![]() ,
,![]() ,直線
,直線![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,若
,若![]() 與
與![]() 關(guān)于點(diǎn)
關(guān)于點(diǎn)![]() 成中心對(duì)稱(chēng),則點(diǎn)
成中心對(duì)稱(chēng),則點(diǎn)![]() 的坐標(biāo)為( )
的坐標(biāo)為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知平面內(nèi)兩點(diǎn)![]() .
.

(1)請(qǐng)用尺規(guī)按下列要求作圖,并保留作圖痕跡;
①連接![]() ;
;
②在線段![]() 的延長(zhǎng)線上取點(diǎn)
的延長(zhǎng)線上取點(diǎn)![]() ,使
,使![]() ;
;
③在線段![]() 的延長(zhǎng)線上取點(diǎn)
的延長(zhǎng)線上取點(diǎn)![]() ,使
,使![]() .
.
(2)請(qǐng)求出線段![]() 與線段
與線段![]() 長(zhǎng)度之間的數(shù)量關(guān)系.
長(zhǎng)度之間的數(shù)量關(guān)系.
(3)如果![]() ,則
,則![]() 的長(zhǎng)度為________,
的長(zhǎng)度為________,![]() 的長(zhǎng)度為________,
的長(zhǎng)度為________,![]() 的長(zhǎng)度為_________.
的長(zhǎng)度為_________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】四邊形ABCD中,對(duì)角線AC、BD相交于點(diǎn)O,下列條件不能判定這個(gè)四邊形是平行四邊形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
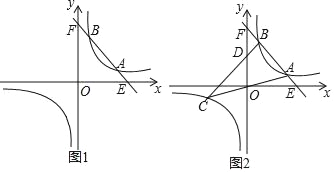
【題目】已知:一次函數(shù)y=﹣2x+10的圖象與反比例函數(shù)y=![]() (k>0)的圖象相交于A、B兩點(diǎn)(A的B的右側(cè)).
(k>0)的圖象相交于A、B兩點(diǎn)(A的B的右側(cè)).
(1)當(dāng)A(4,2)時(shí),求反比例函數(shù)的解析式:
(2)當(dāng)A的橫坐標(biāo)是3,B的橫坐標(biāo)是2時(shí),直線OA與此反比例函數(shù)圖象的另一支交于另一點(diǎn)C,連接BC交y軸于點(diǎn)D.
①求C點(diǎn)的坐標(biāo);
②求D點(diǎn)的坐標(biāo);
③求△ABC的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,AB=DB,∠1=∠2,請(qǐng)問(wèn)添加下面哪個(gè)條件不能判斷△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com