
【題目】如圖,E,F,G,H分別是邊AB,BC,CD,DA的中點. 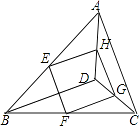
(1)判斷四邊形EFGH的形狀,并證明你的結論;
(2)當BD,AC滿足什么條件時,四邊形EFGH是正方形.(不要求證明)
【答案】
(1)解:在△ABC中,E、F分別是邊AB、BC中點,
所以EF∥AC,且EF= ![]() AC,
AC,
同理有GH∥AC,且GH= ![]() AC,
AC,
∴EF∥GH且EF=GH,
故四邊形EFGH是平行四邊形.
(2)解:EH∥BD且EH= ![]() BD,
BD,
若AC=BD,則有EH=EF,
又因為四邊形EFGH是平行四邊形,
∴四邊形EFGH是菱形,
∵AC⊥BD,
∴∠EHG=90°,
即:當AC=BD且AC⊥BD時,四邊形EFGH是正方形.
【解析】(1)在△ABC中,E、F分別是邊AB、BC中點,得到EF∥AC,且EF= ![]() AC,GH∥AC,且GH=
AC,GH∥AC,且GH= ![]() AC,得到四邊形EFGH是平行四邊形;(2)四邊形EFGH是平行四邊形,再由AC=BD,得出EH=EF,從而證得四邊形EFGH是菱形.對角線相等,推知四邊形EFGH是正方形;
AC,得到四邊形EFGH是平行四邊形;(2)四邊形EFGH是平行四邊形,再由AC=BD,得出EH=EF,從而證得四邊形EFGH是菱形.對角線相等,推知四邊形EFGH是正方形;


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】一個四邊形的三個內角的度數依次如下,那么其中是平行四邊形的是( )
A. 88°,108°,88° B. 88°,104°,88°
C. 88°,92°,92° D. 88°,92°,88°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是一個菱形綠地,其周長為40 ![]() m,∠ABC=120°,在其內部有一個四邊形花壇EFGH,其四個頂點恰好在菱形ABCD各邊的中點,現在準備在花壇中種植茉莉花,其單價為10元/m2 , 請問需投資金多少元?(結果保留整數)
m,∠ABC=120°,在其內部有一個四邊形花壇EFGH,其四個頂點恰好在菱形ABCD各邊的中點,現在準備在花壇中種植茉莉花,其單價為10元/m2 , 請問需投資金多少元?(結果保留整數) 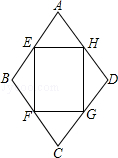
查看答案和解析>>
科目:初中數學 來源: 題型:
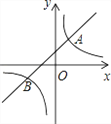
【題目】如圖,已知一次函數![]() (
(![]() 為常數,且
為常數,且![]() )的圖象與反比例函數
)的圖象與反比例函數![]() (
(![]() 為常數,且
為常數,且![]() )的圖象相交于
)的圖象相交于![]() 兩點.
兩點.
(1)求一次函數和反比例函數的解析式;
(2)若![]() 為反比例函數圖象上的三點,且
為反比例函數圖象上的三點,且![]() 請直接寫出
請直接寫出![]() 的大小關系式;
的大小關系式;
(3)結合圖象,請直接寫出關于![]() 的不等式
的不等式![]() >
>![]() 的解集.
的解集.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com