
【題目】若∠A與∠B的兩邊分別垂直,請判斷這兩個角的數量關系.
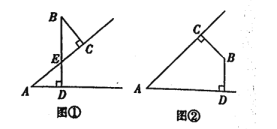
(1)如圖①,∠A與∠B的數量關系是____,如圖②,∠A與∠B的數量關系是____.
(2)請從圖①或圖②中選擇一種情況說明理由。
【答案】(1)∠A=∠B(相等) ,∠A+∠B=180°(互補);(2)見解析.
【解析】
1)如果一個角的兩邊與另一個角的兩邊分別垂直,那么這兩個角的關系是相等或互補;
(2)根據垂直的量相等的角都等于90°,對頂角相等,即可得出∠A=∠B,同樣根據垂直的定義以及四邊形的內角和等于360°,即可得出∠A+∠B=360°-90°-90°=180°.
(1)如圖①,∠A=∠B(相等);如圖②,∠A+∠B=180°(互補);
故答案為:相等,互補;
(2)選題圖①,∵BC⊥AC,BD⊥AD,
∴∠ECB=∠ADE=90°.
又∵∠A=180°-∠EDA-∠AED,∠B=180°-∠BCE-∠BEC,∠AED=∠BEC,
∴∠A=∠B.
選題圖②,∵BC⊥AC,BD⊥AD,
∴∠ECB=∠ADE=90°.
∵四邊形的內角和等于360°,
∴∠A+∠B=360°-90°-90°=180°.


科目:初中數學 來源: 題型:
【題目】把一個含45°角的直角三角板BEF和一個正方形ABCD擺放在一起,使三角板的直角頂點和正方形的頂點B重合,聯結DF,點M,N分別為DF,EF的中點,聯結MA,MN.
(1)如圖1,點E,F分別在正方形的邊CB,AB上,請判斷MA,MN的數量關系和位置關系,直接
寫出結論;
(2)如圖2,點E,F分別在正方形的邊CB,AB的延長線上,其他條件不變,那么你在(1)中得到的兩個結論還成立嗎?若成立,請加以證明;若不成立,請說明理由.
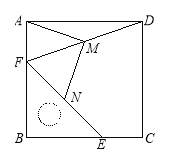
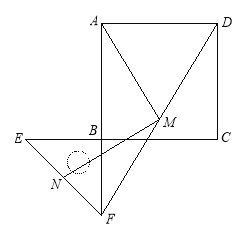
圖1 圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】只用無刻度的直尺作圖(保留作圖痕跡,不要求寫作法)
(1)如圖1,已知∠AOB,OA=OB,點E在OB邊上,其中四邊形AEBF是平行四邊形,請你在圖中畫出∠AOB的平分線.
(2)如圖2,已知E是菱形ABCD中AB邊上的中點,請你在圖中畫出一個矩形EFGH,使得其面積等于菱形ABCD的一半.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系中,點A,B的坐標分別為A(a,0),B(b,0),且a,
b滿足 |a+2|+![]() =0,點C的坐標為(0,3).
=0,點C的坐標為(0,3).
(1)求a,b的值及S三角形ABC;
(2)若點M在x軸上,且S三角形ACM=![]() S三角形ABC,試求點M的坐標.
S三角形ABC,試求點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】南沙群島是我國固有領土,現在我南海漁民要在南沙某海島附近進行捕魚作業,當漁船航行至B處時,測得該島位于正北方向![]() 海里的C處,為了防止某國還巡警干擾,就請求我A處的魚監船前往C處護航,已知C位于A處的北偏東45°方向上,A位于B的北偏西30°的方向上,求A、C之間的距離.
海里的C處,為了防止某國還巡警干擾,就請求我A處的魚監船前往C處護航,已知C位于A處的北偏東45°方向上,A位于B的北偏西30°的方向上,求A、C之間的距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
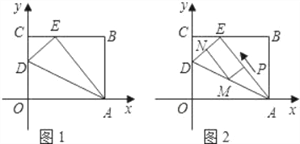
【題目】如圖1,OABC是一張放在平面直角坐標系中的矩形紙片,O為原點,點A在x軸的正半軸上,點C在y軸的正半軸上,OA=5,OC=4.
(1)在OC邊上取一點D,將紙片沿AD翻折,使點O落在BC邊上的點E處,求D,E兩點的坐標;
(2)如圖2,若AE上有一動點P(不與A,E重合)自A點沿AE方向E點勻速運動,運動的速度為每秒1個單位長度,設運動的時間為t秒(0<t<5),過P點作ED的平行線交AD于點M,過點M作AE平行線交DE于點N.求四邊形PMNE的面積S與時間t之間的函數關系式;當t取何值時,s有最大值,最大值是多少?
(3)在(2)的條件下,當t為何值時,以A,M,E為頂點的三角形為等腰三角形,并求出相應的時刻點M的坐標?
查看答案和解析>>
科目:初中數學 來源: 題型:
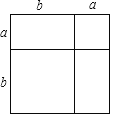
【題目】如圖所示的大正方形是由兩個小正方形和兩個長方形組成.
(1)通過兩種不同的方法計算大正方形的面積,可以得到一個數學等式;
(2)利用(1)中得到的結論,解決下面的問題:若a+b=2,ab=﹣3,
求:①a2+b2;
②a4+b4.
查看答案和解析>>
科目:初中數學 來源: 題型:
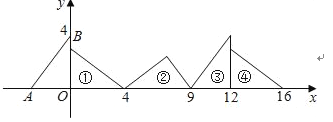
【題目】如圖,在直角坐標系中,已知點A(﹣3,0)、B(0,4),對△OAB連續作旋轉變換,依次得到△1、△2、△3、△4、…,△16的直角頂點的坐標為( )
![]()
A. (60,0) B. (72,0) C. (67![]() ,
,![]() ) D. (79
) D. (79![]() ,
,![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com