
【題目】如圖,二次函數(shù) ![]() 的圖象與x軸與交于點A、點B(2,0),與y軸交于點C,∠ACB=90o.
的圖象與x軸與交于點A、點B(2,0),與y軸交于點C,∠ACB=90o.
(1)求二次函數(shù)解析式;
(2)直線![]() 與
與![]() 軸平行,分別交線段AB、CB于點E、F,且與拋物線交于點P.
軸平行,分別交線段AB、CB于點E、F,且與拋物線交于點P.
①求線段PF取得最大值時,OE的長;
②四邊形ACPB的面積是否存在最大值?如果存在求出此最大值和點P的坐標;如果不存在,說明理由.
(3)不解方程組,直接寫出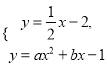 的解.
的解.

【答案】(1)![]() (2)①1;
(2)①1; ![]() (3)
(3)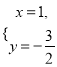
【解析】分析:(1)由△AOC∽△COB得:OA=![]() ,則點A(-
,則點A(-![]() ,0),把A、B代入聯(lián)立方程組,即可求解;(2)①由題意得到直線BC的解析式為:
,0),把A、B代入聯(lián)立方程組,即可求解;(2)①由題意得到直線BC的解析式為: ![]() ,分別設(shè)出點E、F、P的坐標,用含m的式子表示,從而求出線段PF取得最大值時,OE的長;
,分別設(shè)出點E、F、P的坐標,用含m的式子表示,從而求出線段PF取得最大值時,OE的長;
②利用![]() ,得到關(guān)于m的二次函數(shù),配成頂點式,即可求解;(4)根據(jù)函數(shù)圖象可得出結(jié)果.
,得到關(guān)于m的二次函數(shù),配成頂點式,即可求解;(4)根據(jù)函數(shù)圖象可得出結(jié)果.
本題解析:
(1)∵∠ACB=90o, ![]() ,∴
,∴![]()
∴![]() ,∴點A的坐標為
,∴點A的坐標為![]()
∴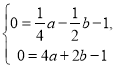 ∴
∴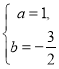
∴![]()
(2)①設(shè)直線BC的解析式為![]() ,由圖象得:
,由圖象得:
![]() , ∴
, ∴![]()
∴直線BC的解析式為: ![]() .
.
如圖,設(shè):E![]() ,則F
,則F![]() ,p
,p![]() ,
,
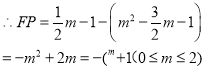
∴當m=1時, ![]()
∴OE=1
② 如圖:
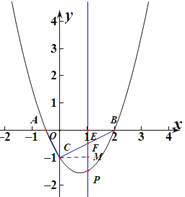
四邊形ACPB的面積存在最大值,
![]()
=![]() ,
,
![]() ,
,
∴P(1, ![]() ).
).
(3)由圖可知:
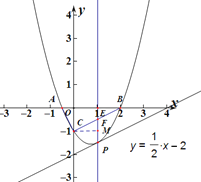
方程組: 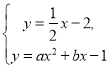 的解為
的解為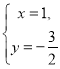


科目:初中數(shù)學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,AC=6,BC=8. 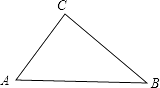
(1)用直尺和圓規(guī)在邊BC上找一點D,使D到AB的距離等于CD.
(2)計算(1)中線段CD的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某校在九年級學生中開展以“每天數(shù)學家庭作業(yè)完成時間”設(shè)置的一個問題,有以下選項:
A.0~0.5小時B.0.5~1個小時 C.1個小時~1.5個小時 D.1.5個小時以上
在隨機調(diào)查了九(1)班學生后,根據(jù)相關(guān)數(shù)據(jù)給出如圖所示的統(tǒng)計圖.
(1)該校九(1)班學生 人;做數(shù)學家庭作業(yè)1.5個小時以上的占 ;
(2)補全頻數(shù)直方圖;
(3)已知該校九年級共400名學生,據(jù)此推算,該校九年級學生中,“做數(shù)學家庭作業(yè)1.5個小時以上”的學生人數(shù).

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
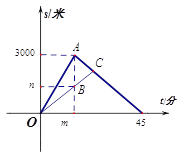
【題目】小明和爸爸周末到濕地公園進行鍛煉,兩人上午9:00從公園入口出發(fā),沿相同路線勻速運動,小明15分鐘后到達目的地,此時爸爸距出發(fā)地1200米,小明到達目的地后立即按原路勻速返回,與爸爸相遇后,和爸爸一起從原路返回出發(fā)地.小明、爸爸在鍛煉過程中離出發(fā)地的路程與小明出發(fā)的時間的函數(shù)關(guān)系如圖.
(1)圖中![]() ,
, ![]() ;
;
(2)求小明和爸爸相遇的時間.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知某種禮炮的升空高度h(m)與飛行時間t(s)的關(guān)系式是h=﹣(t﹣4)2+20.若此禮炮在升空到最高處時引爆,則引爆需要的時間為( )
A.3sB.4sC.5sD.6s
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com