【題目】閱讀理解：
為解方程（x2﹣1）2﹣5（x2﹣1）+4=0，我們可以將x2﹣1視為一個整體，然后設x2﹣1=y，則原方程化為y2﹣5y+4=0，解此方程得：y1=1，y2=4．
當y=1時，x2﹣1═1，∴x=±
．
當y=4時，x2﹣1═4，∴x=±
．
∴原方程的解為：x1=，x2=﹣，x3=，x4=﹣．
以上方法叫做換元法解方程，達到了降次的目的，體現了轉化思想．
運用上述方法解方程：x4﹣8x2+12=0．
53隨堂測系列答案科目：初中數學 來源： 題型：
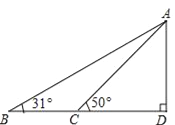
【題目】據調查，超速行駛是引發交通事故的主要原因之一，所以規定以下情境中的速度不得超過15m/s，在一條筆直公路BD的上方A處有一探測儀，如圖，AD=24m，∠D=90°，第一次探測到一輛轎車從B點勻速向D點行駛，測得∠ABD=31°，2秒后到達C點，測得∠ACD=50°.
（1）求B，C的距離．
（2）通過計算，判斷此轎車是否超速．（tan31°≈0.6，tan50°≈1.2，結果精確到1m）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】數學課上，張老師出示了問題：如圖1，四邊形ABCD是正方形，點E是邊BC的中點．∠AEF=90°，且EF交正方形外角∠DCG的角平分線CF于點F，求證：AE=EF．
經過思考，小明展示了一種正確的解題思路：取AB的中點M，連接ME，則AM=EC，易證△AME≌△ECF，所以AE=EF．
在此基礎上，同學們作了進一步的研究：
（1）小穎提出：如圖2，如果把“點E是邊BC的中點”改為“點E是邊BC上（除B，C外）的任意一點”，其它條件不變，那么結論“AE=EF”仍然成立，你認為小穎的觀點正確嗎？如果正確，寫出證明過程；如果不正確，請說明理由；
（2）小華提出：如圖3，點E是BC的延長線上（除C點外）的任意一點，其他條件不變，結論“AE=EF”仍然成立．你認為小華的觀點正確嗎？如果正確，寫出證明過程；如果不正確，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明有5張寫著不同數字的卡片，請按要求抽出卡片，完成下列各問題：
（1）從中取出2張卡片，使這2張卡片上數字的乘積最大，如何抽取？最大值是多少？答：我抽取的2張卡片是________、________，乘積的最大值為________．
（2）從中取出2張卡片，使這2張卡片上數字相除的商最小，如何抽取？最小值是多少？答：我抽取的2張卡片是________、________，商的最小值為________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有20筐白菜，以每筐25千克為標準，超過或不足的千克數分別用正、負數來表示，記錄如下：
（1）20筐白菜中，最重的一筐比最輕的一筐多重多少千克？
（2）與標準重量比較，20筐白菜總計超過或不足多少千克？
（3）若白菜每千克售價2.8元，則出售這20筐白菜可賣多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用小立方塊搭成的幾何體，主視圖和俯視圖如下，
填空：這樣的幾何體有________種可能，它最多需要________小立方塊，最少需要________小立方塊．
請畫出最多和最少時的左視圖．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
