
【題目】解方程.
(1)2(x+2)2-8=0;
(2)x(x-3)=x;
(3)![]() x2=6x-
x2=6x-![]() ;
;
(4)(x+3)2+3(x+3)-4=0.
【答案】(1)x1=0,x2=-4.(2)x1=0,x2=4;(3)x1=![]() ,x2=
,x2=![]() -
-![]() (4)x1=-7,x2=-2.
(4)x1=-7,x2=-2.
【解析】
(1)方程整理后,利用平方根定義開方即可求出解;(2)方程整理后,利用因式分解法求出解即可;(3)方程整理后,利用公式法求出解即可;(4)方程利用因式分解法求出解即可.
(1)整理得(x+2)2=4,即x+2=±2,
∴x1=0,x2=-4.
(2)整理得x(x-3)-x=0,即x(x-3-1)=0,x(x-4)=0,
∴x1=0,x2=4.
(3)整理得![]() x2-6x+
x2-6x+![]() =0,即x2-2
=0,即x2-2![]() x+1=0,
x+1=0,
由求根公式得x1=![]() ,x2=
,x2=![]() -
-![]() .
.
(4)設(shè)x+3=y,則原方程可變?yōu)?/span>y2+3y-4=0,
解得y1=-4,y2=1,當(dāng)y=-4,即x+3=-4時,x=-7,當(dāng)y=1,
即x+3=1時,x=-2.
∴原方程的解為x1=-7,x2=-2.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點E是正方形ABCD外一點,點F是線段AE上一點,△EBF是等腰直角三角形,其中∠EBF=90°,連接CE、CF.
(1)求證:△ABF≌△CBE;
(2)判斷△CEF的形狀,并說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】一袋中裝有形狀大小都相同的四個小球,每個小球上各標(biāo)有一個數(shù)字,分別是1,4,7,8.現(xiàn)規(guī)定從袋中任取一個小球,對應(yīng)的數(shù)字作為一個兩位數(shù)的個位數(shù);然后將小球放回袋中并攪拌均勻,再任取一個小球,對應(yīng)的數(shù)字作為這個兩位數(shù)的十位數(shù).
(1)寫出按上述規(guī)定得到所有可能的兩位數(shù);
(2)從這些兩位數(shù)中任取一個,求其算術(shù)平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】你能求![]() 的值嗎?遇到這樣的問題,我們可以先思考一下,從簡單的情形入手.先分別計算下列各式的值.
的值嗎?遇到這樣的問題,我們可以先思考一下,從簡單的情形入手.先分別計算下列各式的值.
①![]()
②![]()
③![]() ……
……
(1)由此我們可以得到:![]()
請你利用上面的結(jié)論,再完成下面兩題的計算:
(2)250+249+248+…+22+2+1
(3)若![]() ,求x2020的值
,求x2020的值
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,錨標(biāo)浮筒是打撈作業(yè)中用來標(biāo)記錨或沉船位置的,它的上下兩部分是圓柱,中間是一個圓柱(如圖,單位:mm).電鍍時,如果每平方米用鋅0.11kg,要電鍍1000個這樣的錨標(biāo)浮筒需要用多少鋅?(精確到1kg)
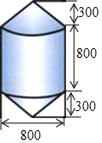
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在下列各組條件中,不能說明![]() 的是( )
的是( )
A.AB=DE,∠B=∠E,∠C=∠FB.AB=DE,∠A=∠D,∠B=∠E
C.AC=DF,BC=EF,∠A=∠DD.AB=DE,BC=EF,AC=ED
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】一點A從數(shù)軸上表示+2的點開始移動,第一次先向左移動1個單位,再向右移動2個單位;第二次先向左移動3個單位,再向右移動4個單位;第三次先向左移動5個單位,再向右移動6個單位……
(1)寫出第一次移動后這個點在數(shù)軸上表示的數(shù)為 ;
(2)寫出第二次移動后這個點在數(shù)軸上表示的數(shù)為 ;
(3)寫出第五次移動后這個點在數(shù)軸上表示的數(shù)為 ;
(4)寫出第![]() 次移動結(jié)果這個點在數(shù)軸上表示的數(shù)為 ;
次移動結(jié)果這個點在數(shù)軸上表示的數(shù)為 ;
(5)如果第![]() 次移動后這個點在數(shù)軸上表示的數(shù)為56,求
次移動后這個點在數(shù)軸上表示的數(shù)為56,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線y=![]() x2+bx﹣2與x軸交于A、B兩點,與y軸交于C點,且A(﹣1,0).
x2+bx﹣2與x軸交于A、B兩點,與y軸交于C點,且A(﹣1,0).
(1)求拋物線的解析式及頂點D的坐標(biāo);
(2)判斷△ABC的形狀,證明你的結(jié)論;
(3)點M是x軸上的一個動點,當(dāng)△DCM的周長最小時,求點M的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知直線l分別與x軸,y軸交于A,B兩點,與雙曲線(k≠0,x>0)分別交于D,E兩點.若點D的坐標(biāo)為((3.1),點E的坐標(biāo)為(1,n).
(1)分別求出直線l與雙曲線的解析式;
(2)求△EOD的面積;
(3)若將直線l向下平移m(m>O)個單位,當(dāng)m為何位時,直線l與雙曲線有且只有一個交點.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com