【題目】在四邊形
中，
與
的角平分線交于點
，
，過點
作
交
于點
，
，
，連接
，
，則
__________．
科目：初中數學 來源： 題型：
【題目】閱讀材料： 小明在學習二次根式后，發(fā)現一些含根號的式子可以寫成另一個式子的平方，如：
，善于思考的小明進行了以下探索：
設
（其中
均為整數），則有
．
∴
．這樣小明就找到了一種把部分
的式子化為平方式的方法．
請你仿照小明的方法探索并解決下列問題：
當均為正整數時，若
，用含m、n的式子分別表示
，得
＝ ，
＝ ；
（2）利用所探索的結論，找一組正整數，填空： ＋ ＝( ＋ 
)2；
（3）若
，且均為正整數，求的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知反比例函數 
，則下列結論不正確的是( )
A.圖象必經過點（-1，5）
B.圖象的兩個分支分布在第二、四象限
C.y隨x的增大而增大
D.若x＞1，則－5＜y＜0
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下面說法正確的個數有（ ）
（1）二元一次方程組的兩個方程的所有解，叫做二元一次方程組的解；
（2）如果
，則
；
（3）三角形的外角等于與它不相鄰的兩個內角的和；
（4）多邊形內角和等于
；
（5）一組數據1，2，3，4，5的眾數是0
A.0個B.1個C.2個D.3個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，將兩個完全相同的三角形紙片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°.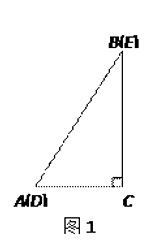
（1）操作發(fā)現
如圖2，固定△ABC，使△DEC繞點C旋轉，當點D恰好落在AB邊上時，填空：
①線段DE與AC的位置關系是；
②設△BDC的面積為S1 ， △AEC的面積為S2 ， 則S1與S2的數量關系是.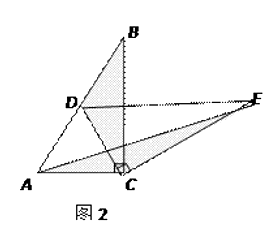
（2）猜想論證
當△DEC繞點C旋轉到圖3所示的位置時，小明猜想（1）中S1與S2的數量關系仍然成立，并嘗試分別作出了△BDC和△AEC中BC、CE邊上的高，請你證明小明的猜想.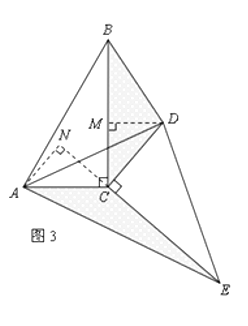
（3）拓展探究
已知∠ABC=60°，點D是其角平分線上一點，BD=CD=4，DE//AB交BC于點E（如圖4）.若在射線BA上存在點F，使 
，請直接寫出相應的BF的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】△ABC在平面直角坐標系中，且A
、B
、C
.將其平移后得到
，若A，B的對應點是
，
，C的對應點
的坐標是
.
（1）在平面直角坐標系中畫出△ABC；
（2）寫出點的坐標是_____________,坐標是___________;
（3）此次平移也可看作向________平移了____________個單位長度，再向_______平移了______個單位長度得到△ABC.
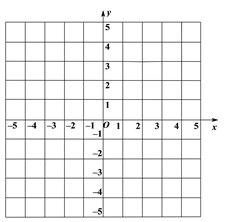
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們知道，有理數包括整數、有限小數和無限循環(huán)小數，事實上，所有的有理數都可以化為分數形式(整數可看作分母為1的分數)，那么無限循環(huán)小數如何表示為分數形式呢？請看以下示例：
例：將
化為分數形式，
由于
，設
，①
得
，②
②①得
,解得
,于是得
.
同理可得
,
.
根據以上閱讀,回答下列問題：(以下計算結果均用最簡分數表示)
（類比應用）
(1)
；
(2)將
化為分數形式，寫出推導過程；
（遷移提升）
(3)
，
；(注
,
）
（拓展發(fā)現）
(4)若已知
，則
.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有一批共享單車需要維修，維修后繼續(xù)投放騎用，現有甲、乙兩人做維修，甲每天維修16輛，乙每天維修的車輛比甲多8輛，甲單獨維修完成這批共享單車比乙單獨維修完多用20天，公司每天付甲80元維修費，付乙120元維修費．
（1）問需要維修的這批共享單車共有多少輛？
（2）在維修過程中，公司要派一名人員進行質量監(jiān)督，公司負擔他每天10元補助費，現有三種維修方案：①由甲單獨維修；
②由乙單獨維修；
③甲、乙合作同時維修，你認為哪種方案最省錢，為什么？
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
