【題目】計算：(1) 
；(2) 
；
(3)
；(4) 
【答案】（1）－3；（2）
；（3）
；（4）
【解析】
有理數的加減混合運算，可以利用加法的運算律將負數與正數分開分別相加，這樣可以減少異號兩數相加易犯的錯誤，整式加減運算先去括號，然后合并同類項即可.
解：（1）原式=6—0.5—10＋1.5=（6－10）＋（－0.5＋1.5）=－4＋1=－3；
（2）原式=－3－
＋4 =（－3＋4）－ =1－ =；
(3)原式=
=
=
=
；
(4)原式=
=
.
“點睛”本題在運算過程中第一步是將加減統一成加法，第二步是省略加號寫成代數和的形式，第三步是運用了加法交換律，第四步是運用了加法結合律，后面是利用加法法則，通過運算過程我們還可以看到加法的運算律在運算中的重要作用.
贏在課堂名師課時計劃系列答案
天天向上課時同步訓練系列答案科目：初中數學 來源： 題型：
【題目】若x=1，y=
，則x2+4xy+4y2的值是（ ）
A. 2 B. 4 C. 32 D. 12
【答案】B
【解析】解析：x2+4xy+4y2=（x+2y）2=
=4.故選B.
【題型】單選題
【結束】
9
【題目】下列因式分解，正確的是（ ）
A. x2y2-z2=x2（y+z）（y-z） B. -x2y+4xy-5y=-y（x2+4x+5）
C. （x+2）2-9=（x+5）（x-1） D. 9-12a+4a2=-（3-2a）2
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】周末，小李從家里出發騎車到少年宮學習繪畫，學完后立即回家，他離家的距離y(km)與時間x(h)之間的函數關系如圖所示，有下列結論：①他家離少年宮30km；②他在少年宮一共停留了3h；③他返回家時，離家的距離y(km)與時間x(h)之間的函數表達式是y＝－20x＋110；④當他離家的距離y＝10時，時間x＝
.其中正確的是________(填序號)．
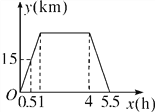
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在社會主義新農村建設中，衢州某鄉鎮決定對A、B兩村之間的公路進行改造，并有甲工程隊從A村向B村方向修筑，乙工程隊從B村向A村方向修筑．已知甲工程隊先施工3天，乙工程隊再開始施工．乙工程隊施工幾天后因另有任務提前離開，余下的任務有甲工程隊單獨完成，直到公路修通．下圖是甲乙兩個工程隊修公路的長度y（米）與施工時間x（天）之間的函數圖象，請根據圖象所提供的信息解答下列問題：
（1）乙工程隊每天修公路多少米？
（2）分別求甲、乙工程隊修公路的長度y（米）與施工時間x（天）之間的函數關系式．
（3）若該項工程由甲、乙兩工程隊一直合作施工，需幾天完成？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某地A、B兩村盛產柑橘，A村有柑橘200噸，B村有柑橘300噸，現將這些柑橘運到C、D兩個冷藏倉庫．已知C倉庫可儲存240噸，D倉庫可儲存260噸，從A村運往C、D兩處的費用分別為每噸20元、25元，從B村運往C、D兩處的費用分別為每噸15元、18元．設從A村運往C倉庫的柑橘重量為x噸，A、B兩村運往兩倉庫的柑橘運輸費用分別為yA元、yB元．
(1)請填寫下表，并求出yA、yB與x之間的函數表達式；
(2)試討論A、B兩村中，哪個村的運費較少；
(3)考慮到B村的經濟承受能力，B村的柑橘運費不得超過4830元，在這種情況下，請問怎樣調運才能使兩村運費之和最小？求出這個最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖：三角形
中，
、
分別是
和
的平分線，、相交于點
（知識鏈接：三角形三個內角的和是180°。如圖
是三角形的一個內角）
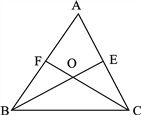
（1）如果
°求
的度數。
（2）如果
°直接寫出的度數
（3）探求和的關系（用等式表示），并簡要說明理由。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為發展校園足球運動，某縣城區四校決定聯合購買一批足球運動裝備，市場調查發現：甲、乙兩商場以同樣的價格出售同種品牌的足球隊服和足球，已知每套隊服比每個足球多50元，兩套隊服與三個足球的費用相等，經洽談，甲商場優惠方案是：每購買十套隊服，送一個足球；乙商場優惠方案是：若購買隊服超過80套，則購買足球打八折．
（1）求每套隊服和每個足球的價格是多少？
（2）若城區四校聯合購買100套隊服和a個足球，請用含a的式子分別表示出到甲商場和乙商場購買裝備所花的費用；
（3）假如你是本次購買任務的負責人，你認為到哪家商場購買比較合算？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形ABCD中，AB=8，BC=6，點E在邊AB上，點F在邊CD上，點G、H在對角線AC上，若四邊形EGFH是菱形，則AE的長是（ ） 
A.6
B.6.25
C.6.5
D.7
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，把矩形紙片ABCD置于直角坐標系中，AB∥x軸，BC∥y軸，AB=4，BC=3，點B（5，1）翻折矩形紙片使點A落在對角線DB上的H處得折痕DG．
（1）求AG的長；
（2）在坐標平面內存在點M（m，﹣1）使AM+CM最小，求出這個最小值；
（3）求線段GH所在直線的解析式．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com