
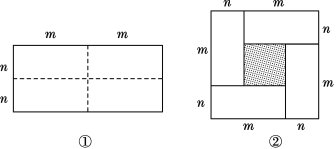
【題目】圖①是一個長為2m、寬為2n的長方形,沿圖中虛線用剪刀把它均分成四個小長方形,然后按圖②的形狀拼成一個正方形.
(1)你認為圖②中的陰影部分的正方形的邊長等于多少?
(2)請用兩種不同的方法求圖②中陰影部分的面積.
(3)觀察圖②你能寫出下列三個代數式之間的等量關系嗎?
代數式:(m+n)2,(m-n)2,mn.
(4)根據(3)題中的等量關系,解決如下問題:
已知a+b=7,ab=5,求(a-b)2的值.(寫出過程)
【答案】解:(1)m-n;(2)詳見解析;(3)(m+n)2=(m-n)2+4mn;(4)29.
【解析】
(1)觀察可得陰影部分的正方形邊長是m-n;
(2)方法1:邊長為m+n的大正方形的面積減去4個長為m,寬為n的小長方形面積;
方法2:邊長為m+n的大正方形的面積減去長為2m,寬為2n的長方形面積;
(3)由(2)可得結論(m+n)2=(m-n)2+4mn;
(4)由(a-b)2=(a+b)2-4ab求解.
(1)陰影部分的正方形邊長是m-n.
(2)陰影部分的面積就等于邊長為m-n的小正方形的面積,
方法1:邊長為m+n的大正方形的面積減去長為2m,寬為2n的長方形面積,
即(m-n)2=(m+n)2-4mn;
方法2:邊長為m+n的大正方形的面積減去長為2m,寬為2n的長方形面積,
即(m-n)2=(m+n)2-2m2n=(m+n)2-4mn;
(3)(m+n)2=(m-n)2+4mn.
(4)(a-b)2=(a+b)2-4ab=49-4×5=29.


 同步輕松練習系列答案
同步輕松練習系列答案 課課通課程標準思維方法與能力訓練系列答案
課課通課程標準思維方法與能力訓練系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線y=2x+3與y軸交于A點,與反比例函數y= ![]() (x>0)的圖象交于點B,過點B作BC⊥x軸于點C,且C點的坐標為(1,0).
(x>0)的圖象交于點B,過點B作BC⊥x軸于點C,且C點的坐標為(1,0). 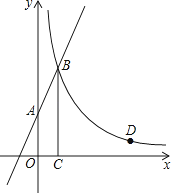
(1)求反比例函數的解析式;
(2)點D(a,1)是反比例函數y= ![]() (x>0)圖象上的點,在x軸上是否存在點P,使得PB+PD最小?若存在,求出點P的坐標;若不存在,請說明理由.
(x>0)圖象上的點,在x軸上是否存在點P,使得PB+PD最小?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:已知正方形的邊長為4,甲、乙兩動點分別從正方形ABCD的頂點A、C同時沿正方形的邊開始移動,甲點依順時針方向環行,乙點依逆時針方向環行,若乙的速度是甲的速度的3倍,則它們第2018次相遇在邊 ( )上.
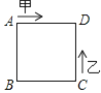
A. AB B. BC C. CD D. DA
查看答案和解析>>
科目:初中數學 來源: 題型:
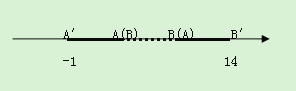
【題目】(1)如圖,在數軸上有一小木棒AB,若平移木棒,使B落在A處,則A′所表示的數為 -1,若將A落在B處時,則B′所表示的數14,它的兩個端點A、B所表示的數分別是 、 .
(2)老師給東東出了一道關于年齡的數學題:我像你那么小時,你才兩歲;你像我那么大時,我已經44歲了,你猜我有多少歲?親愛的同學,你能不能利用上一題的方法幫助小東求出老師的年齡呢?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com