
【題目】在平面直角坐標系![]() 中,
中,![]() 的半徑為
的半徑為![]() ,點
,點![]() 與圓心
與圓心![]() 不重合,給出如下定義:若在
不重合,給出如下定義:若在![]() 上存在一點
上存在一點![]() ,使
,使![]() ,則稱點
,則稱點![]() 為
為![]() 的特征點.
的特征點.
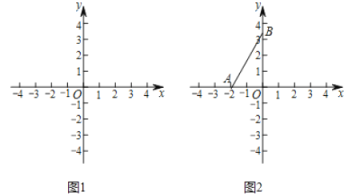
(1)當![]() 的半徑為1時,如圖1.
的半徑為1時,如圖1.
①在點![]() ,
,![]() ,
,![]() 中,
中,![]() 的特征點是__________.
的特征點是__________.
②點![]() 在直線
在直線![]() 上,若點
上,若點![]() 為
為![]() 的特征點,求
的特征點,求![]() 的取值范圍.
的取值范圍.
(2)如圖2,![]() 的圓心在
的圓心在![]() 軸上,半徑為2,點
軸上,半徑為2,點![]() ,
,![]() .若線段
.若線段![]() 上的所有點都是
上的所有點都是![]() 的特征點,直接寫出圓心
的特征點,直接寫出圓心![]() 的橫坐標
的橫坐標![]() 的取值范圍.
的取值范圍.
【答案】(1)①![]() ,
,![]() ;②
;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①根據⊙O的特征點的定義,如果0<OP≤2r(r為⊙O的半徑),則點P是⊙O的特征點;
②分兩種情形考慮問題:如圖1中,當b>0時,設直線y=-![]() x+b與1為半徑的⊙O相切于點C,與y軸交于點E,與x軸交于點F.解直角三角形求出OE即可,當b<0時,根據對稱性可得結論;
x+b與1為半徑的⊙O相切于點C,與y軸交于點E,與x軸交于點F.解直角三角形求出OE即可,當b<0時,根據對稱性可得結論;
(2)如圖中,取點K(2,0),連接BK.由題意滿足條件點C到點B的距離小于等于4且點C到點A的距離小于等于4(點A除外),由此即可解決問題;
(1)①由題意當0<OP≤2r(r為⊙O的半徑),則點P是⊙O的特征點,
∵![]() ,
,
![]() =2,
=2,
![]() ,
,
∴![]() ,
,![]() 是特征點,
是特征點,
故答案為:![]() ,
,![]() ;
;
②當![]() 時,設直線
時,設直線![]() 與以1為半徑的
與以1為半徑的![]() 相切于點
相切于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,
,
∴![]() ,
,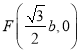 ,
,![]() ,
,
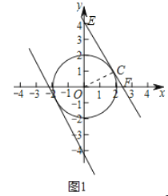
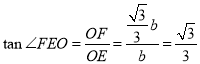 ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
當![]() 時,由對稱性可知:
時,由對稱性可知:![]() ,
,
∴![]() 的取值范圍是
的取值范圍是![]() ;
;
(2)如圖中,取點K(2,0),連接BK,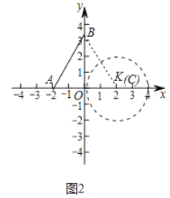
∵點A、B、K的坐標分別為(-2,0),(0,2![]() ),(2,0),
),(2,0),
∴OA=2,OB=2![]() ,OK=2,
,OK=2,
∴AB=![]() ,AK=AO+OK=4,
,AK=AO+OK=4,
![]() ,
,
∴![]() ,
,
∴△ABK是邊長為4的等邊三角形,
∵線段AB上的所有點都是⊙C的特征點,
∴點C到點B的距離小于等于4且點C到點A的距離小于等于4(點A除外),
∴點C在線段AK上(點A除外),
∴滿足條件的m的值為![]() .
.


科目:初中數學 來源: 題型:
【題目】某年五月,我國南方某省A、B兩市遭受嚴重洪澇災害,鄰近縣市C、D決定調運物資支援A、B兩市災區.已知C市有救災物資240噸,D市有救災物資260噸,現將這些救災物資全部調往A、B兩市,A市需要的物資比B市需要的物資少100噸.已知從C市運往A、B兩市的費用分別為每噸20元和25元,從D市運往往A、B兩市的費用分別為每噸15元和30元,設從D市運往B市的救災物資為x噸.
(1)A、B兩市各需救災物資多少噸?
(2)設C、D兩市的總運費為w元,求w與x之間的函數關系式,并寫出自變量x的取值范圍;
(3)經過搶修,從D市到B市的路況得到了改善,縮短了運輸時間,運費每噸減少m元(m>0),其余路線運費不變.若C、D兩市的總運費的最小值不小于10320元,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
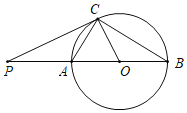
【題目】如圖,已知AB是⊙O的直徑,AC是弦,點P是BA延長線上一點,連接PC、BC,∠PCA=∠B.
(1)求證:PC是⊙O的切線;
(2)若PC=4,PA=2,求直徑AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
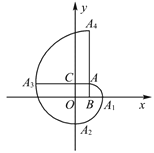
【題目】如圖,在平面直角坐標系中,四邊形![]() 是正方形,點
是正方形,點![]() 的坐標為
的坐標為![]() ,弧
,弧![]() 是以點
是以點![]() 為圓心,
為圓心,![]() 為半徑的圓弧;弧
為半徑的圓弧;弧![]() 是以點
是以點![]() 為圓心,
為圓心,![]() 為半徑的圓弧;弧
為半徑的圓弧;弧![]() 是以點
是以點![]() 為圓心,
為圓心,![]() 為半徑的圓弧;弧
為半徑的圓弧;弧![]() 是以點
是以點![]() 為圓心,
為圓心,![]() 為半徑的圓弧,繼續以點
為半徑的圓弧,繼續以點![]() 為圓心,按上述作法得到的曲線
為圓心,按上述作法得到的曲線![]() …,稱為正方形的“漸開線”,則點
…,稱為正方形的“漸開線”,則點![]() 的坐標是______.
的坐標是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校運動會的立定跳遠和1分鐘跳繩兩個單項比賽分成預賽和決賽兩個階段.下表為參加這兩項比賽的10名學生的預賽成績:
學生編號 成績 項目 | 3104 | 3508 | 3115 | 3406 | 3317 | 3413 | 3218 | 3307 | 3519 | 3210 |
立定跳遠(單位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
1分鐘跳繩(單位:次) | 163 |
| 175 | 160 | 163 | 172 | 170 |
|
| 165 |
在這10名學生中,同時進入兩項決賽的只有6人,進入立定跳遠決賽的有8![]() 的值是__________.
的值是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有這樣一個問題:探究函數![]() 的圖象和性質.小奧根據學習函數的經驗,對函數
的圖象和性質.小奧根據學習函數的經驗,對函數![]() 的圖象和性質進行了探究.下面是小奧的探究過程,請補充完整:
的圖象和性質進行了探究.下面是小奧的探究過程,請補充完整:
(1)函數![]() 的自變量
的自變量![]() 的取值范圍是_________;
的取值范圍是_________;
(2)下表是![]() 與
與![]() 的幾組對應值,則
的幾組對應值,則![]() 的值為______,
的值為______,![]() 的值為______;
的值為______;
| … |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | … |
| … |
|
|
|
|
|
|
|
| 2 |
|
|
| … |
(3)如右圖,在平面直角坐標系![]() 中,描出了以上表中各組對應值為坐標的點.根據描出的點,畫出該函數的圖象;
中,描出了以上表中各組對應值為坐標的點.根據描出的點,畫出該函數的圖象;
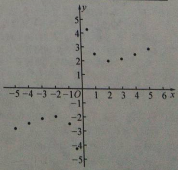
(4)進一步探究發現,該函數圖象在第一象限內的最低點的坐標是![]() .結合函數圖象,寫出該函數的其他兩條性質:①_________,②_________.
.結合函數圖象,寫出該函數的其他兩條性質:①_________,②_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
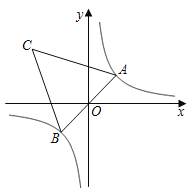
【題目】如圖,在反比例函數![]() 的圖象上有一動點
的圖象上有一動點![]() ,連接
,連接![]() 并延長交圖象的另一支于點
并延長交圖象的另一支于點![]() ,在第二象限內有一點
,在第二象限內有一點![]() ,滿足
,滿足![]() ,當點
,當點![]() 運動時,點
運動時,點![]() 始終在函數
始終在函數![]() 的圖象上運動,若
的圖象上運動,若![]() ,則
,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
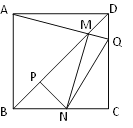
【題目】如圖,邊長一定的正方形ABCD,Q是CD上一動點,AQ交BD于點M,過M作MN⊥AQ交BC于N點,作NP⊥BD于點P,連接NQ,下列結論:①AM=MN;
②MP=![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④![]() 為定值。其中一定成立的是_______.
為定值。其中一定成立的是_______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com