
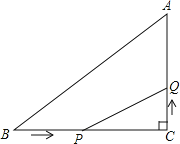
【題目】如圖,△ABC中,∠C=90°,BC=7cm,AC=5,點P從B點出發,沿BC方向以2m/s的速度移動,點Q從C出發,沿CA方向以1m/s的速度移動.
(1)若P、Q同時分別從B、C出發,那么幾秒后,△PCQ的面積等于4?
(2)若P、Q同時分別從B、C出發,那么幾秒后,PQ的長度等于5?
(3)△PCQ的面積何時最大,最大面積是多少?
【答案】(1)若P、Q同時分別從B、C出發,那么![]() 、
、![]() 秒后,△PCQ的面積等于4;
秒后,△PCQ的面積等于4;
(2)![]() 秒后,PQ的長度等于5;
秒后,PQ的長度等于5;
(3)當t=![]() 時△PCQ的面積最大,最大面積為
時△PCQ的面積最大,最大面積為![]() .
.
【解析】
試題分析:(1)分別表示出線段CP和線段CQ的長,利用三角形的面積公式列出方程求解即可;
(2)表示出線段CP和CQ后利用勾股定理列出方程求解即可;
(3)列出△PCQ的面積關于t的函數解析式,配方可得最大值.
解:(1)設t秒后△PCQ的面積等于4,根據題意得:CQ=t,BP=2t,則CP=7﹣2t,
![]() CQCP=
CQCP=![]() ×t(7﹣2t)=4,
×t(7﹣2t)=4,
整理,得:t1=![]() ,t2=
,t2=![]() ,
,
故若P、Q同時分別從B、C出發,那么![]() 、
、![]() 秒后,△PCQ的面積等于4;
秒后,△PCQ的面積等于4;
(2)若PQ的長度等于5,則PC2+QC2=PQ2,
即:(7﹣2t)2+t2=25,
整理,得:5t2﹣28t+24=0,
解得:t1=![]() ,t2=
,t2=![]() ,
,
∵CP=7﹣2t≥0,即t≤3.5,
∴t=![]() >3.5,舍去,
>3.5,舍去,
故那么![]() 秒后,PQ的長度等于5;
秒后,PQ的長度等于5;
(3)由(1)知△PCQ的面積S=![]() ×t(7﹣2t)=﹣(t﹣
×t(7﹣2t)=﹣(t﹣![]() )2+
)2+![]() ,
,
當t=![]() 時,S取得最大值,最大值為
時,S取得最大值,最大值為![]() ,
,
故當t=![]() 時△PCQ的面積最大,最大面積為
時△PCQ的面積最大,最大面積為![]() .
.


科目:初中數學 來源: 題型:
【題目】某商品的價格標簽已丟失,售貨員只知道“它的進價為80元,打七折售出后,仍可獲利4元”,你認為售貨員應標在標簽上的價格是______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1所示,邊長為a的大正方形中有一個邊長為b的小正方形,如圖2是由圖1中陰影部分拼成的一個長方形。
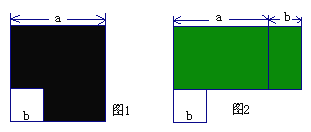
(1)請你分別表示出這兩個圖形中陰影部分的面積: , ;
(2)請問以上結果可以驗證哪個乘法公式? ;
(3)試利用這個公式計算:
①、![]() ②、
②、 ![]()
③、![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】x表示一個兩位數,y表示一個三位數,如果把x放在y的左邊組成一個五位數,那么這個五位數就可以表示為( )
A. xy B. x+y C. 1 000x+y D. 10x+y
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一張對邊互相平行的紙條,折成如圖所示,EF是折痕,若∠EFB=32°,則下列結論正確的有( )
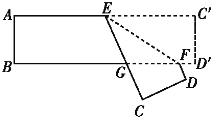
(1)∠C′EF=32°;(2)∠AEC=148°;
(3)∠BGE=64°; (4)∠BFD=116°.
(A)1個 (B)2個 (C)3個 (D)4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A,B,C,D,E五名學生猜測自己的數學成績. A說:“如果我得優,那么B也得優.” B說:“如果我得優,那么C也得優.” C說:“如果我得優,那么D也得優.” D說:“如果我得優,那么E也得優.” 大家都沒有說錯,但只有三個人得優,請問:得優的是哪三個人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com