【題目】在同一平面直角坐標系中，函數y=mx+m與y= 
（m≠0）的圖象可能是（ ）
A.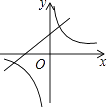
B.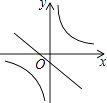
C.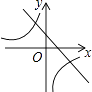
D.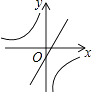
ABC考王全優卷系列答案科目：初中數學 來源： 題型：
【題目】在某項針對18～35歲的青年人每天發微博數量的調查中，設一個人的“日均發微博條數”為m，規定：當m≥10時為A級，當5≤m＜10時為B級，當0≤m＜5時為C級．現隨機抽取30個符合年齡條件的青年人開展每人“日均發微博條數”的調查，所抽青年人的“日均發微博條數”的數據如下表：
11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 |
2 | 8 | 10 | 17 | 6 | 13 | 7 | 5 | 7 | 3 |
12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
（1）求樣本數據中為A級的頻率；
（2）試估計1000個18～35歲的青年人中“日均發微博條數”為A級的人數；
（3）從樣本數據為C級的人中隨機抽取2人，用列舉法求抽得2個人的“日均發微博條數”都是3的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，已知AB為⊙O的直徑，點C為 
的中點，點D在 
上，連接BD、CD、BC、AD、BC與AD相交于點E． 
（1）求證：∠C+∠CBD=∠CBA；
（2）如圖2，過點C作CD的垂線，分別與AD，AB，⊙O相交于點F、G、H，求證：AF=BD；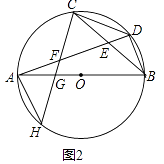 
（3）如圖3，在（2）的條件下，連接BF，若BF=BC，△CEF的面積等于3，求FG的長．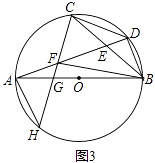 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，是某副食品公司銷售糖果的總利潤y（元）與銷售量x（千克）之間的函數圖象（總利潤=總銷售額﹣總成本），該公司想通過“不改變總成本，提高糖果售價”的方案解決銷售不佳的現狀，下面給出的四個圖象，虛線均表示新的銷售方案中總利潤與銷售量之間的函數圖象，則能反映該公司改進方案的是（ ） 
A.
B.
C.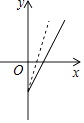
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點P在射線AB的上方，且∠PAB=45°，PA=2，點M是射線AB上的動點（點M不與點A重合），現將點P繞點A按順時針方向旋轉60°，到點Q，將點M繞點P按逆時針方向旋轉60°到點N，連結AQ，PM，PN，作直線QN．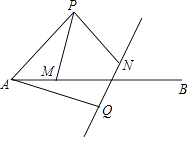 
（1）求證：AM=QN；
（2）直線QN與以點P為圓心，以PN的長為半徑的圓是否存在相切的情況？若存在，請求出此時AM的長，若不存在，請說明理由；
（3）當以點P為圓心，以PN的長為半徑的圓經過點Q時，直接寫出劣弧NQ與兩條半徑所圍成的扇形的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】△ABC的頂點坐標為A（﹣2，3）、B（﹣3，1）、C（﹣1，2），以坐標原點O為旋轉中心，順時針旋轉90°，得到△A′B′C′，點B′、C′分別是點B、C的對應點． 
（1）求過點B′的反比例函數解析式；
（2）求線段CC′的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，輪船甲位于碼頭O的正西方向A處，輪船乙位于碼頭O的正北方向C處，測得∠CAO=45°，輪船甲自西向東勻速行駛，同時輪船乙沿正北方向勻速行駛，它們的速度分別為45km/h和36km/h，經過0.1h，輪船甲行駛至B處，輪船乙行駛至D處，測得∠DBO=58°，此時B處距離碼頭O多遠？（參考數據：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
