
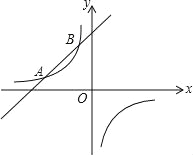
【題目】如圖,已知反比例函數y1=![]() (k≠0)的圖象經過點(8,-
(k≠0)的圖象經過點(8,-![]() ),直線y2=x+b與反比例函數圖象相交于點A和點B(m,4).
),直線y2=x+b與反比例函數圖象相交于點A和點B(m,4).
(1)求上述反比例函數和直線的解析式;
(2)當y1<y2時,請直接寫出x的取值范圍.
【答案】(1)反比例函數解析式為y1=﹣![]() ;直線的解析式為y2=x+5.(2)﹣4<x<﹣1或x>0.
;直線的解析式為y2=x+5.(2)﹣4<x<﹣1或x>0.
.
【解析】(1)∵反比例函數y1=![]() (k≠0)的圖象經過點A(8,﹣
(k≠0)的圖象經過點A(8,﹣![]() ),
),
∴﹣![]() =
=![]() ,∴k=﹣4,
,∴k=﹣4,
∴反比例函數解析式為y1=﹣![]() . .................1分
. .................1分
∵點B(m,4)在反比例函數解析式為y1=﹣![]() 上,
上,
∴4=﹣![]() ,∴m=﹣1, .................2分
,∴m=﹣1, .................2分
又B(﹣1,4)在y2=x+b上,∴4=﹣1+b,∴b=5, .................3分
∴直線的解析式為y2=x+5. .................4分
(2)由圖象可知,當y1<y2時x的取值范圍﹣4<x<﹣1或x>0.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】我們知道,任意一個正整數n都可以進行這樣的分解:n=p×q(p,q是正整數,且p≤q),在n的所有這種分解中,如果p,q兩因數之差的絕對值最小,我們就稱p×q是n的最佳分解.并規定:F(n)= ![]() .例如12可以分解成1×12,2×6或3×4,因為12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)=
.例如12可以分解成1×12,2×6或3×4,因為12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)= ![]() .
.
(1)如果一個正整數a是另外一個正整數b的平方,我們稱正整數a是完全平方數.則對任意一個完全平方數m,F(m)=;
(2)如果一個兩位正整數t,t=10x+y(1≤x≤y≤9,x,y為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為18,那么我們稱這個數t為“吉祥數”,求所有“吉祥數”中F(t)的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題:①無理數都是無限小數;② ![]() 的平方根是±4;③等腰三角形的對稱軸是它頂角的平分線;④三角形三邊垂直平分線的交點一定在這個三角形的內部,正確的有( )
的平方根是±4;③等腰三角形的對稱軸是它頂角的平分線;④三角形三邊垂直平分線的交點一定在這個三角形的內部,正確的有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分線,點O在AB上,⊙O經過B,D兩點,交BC于點E.
(1)求證:AC是⊙O的切線;
(2)若AB=6,sin∠BAC=![]() ,求BE的長.
,求BE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,直徑AB⊥CD,垂足為E,點M在OC上,AM的延長線交⊙O于點G,交過C的直線于F,∠1=∠2,連結CB與DG交于點N.
(1)求證:CF是⊙O的切線;
(2)求證:△ACM∽△DCN;
(3)若點M是CO的中點,⊙O的半徑為4,cos∠BOC=![]() ,求BN的長.
,求BN的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com