
【題目】如圖所示,三角形ABC的面積為4cm2.AP垂直∠B的平分線BP于點(diǎn)P.則三角形PBC的面積是__.

【答案】2cm2
【解析】
過點(diǎn)P作PE⊥BP,垂足為P,交BC于點(diǎn)E,由角平分線的定義可知∠ABP=∠EBP,結(jié)合BP=BP以及∠APB=∠EPB=90°即可證出△ABP≌△EBP(ASA),進(jìn)而可得出AP=EP,根據(jù)三角形的面積即可得出S△APC=S△EPC,再根據(jù)S△PBC=S△BPE+S△EPC=![]() S△ABC即可得出結(jié)論.
S△ABC即可得出結(jié)論.
延長AP,交BC于點(diǎn)E,如圖所示。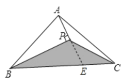
∵AP垂直∠B的平分線BP于點(diǎn)P,
∴∠ABP=∠EBP.
在△ABP和△EBP中, 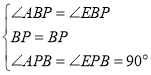 ,
,
∴△ABP≌△EBP(ASA),
∴AP=EP.
∵△APC和△EPC等底同高,
S△PBC=S△BPE+S△EPC=![]() S△ABC=2(cm2).
S△ABC=2(cm2).
故答案為2cm2.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)M是等邊△ABD中邊AB上任意一點(diǎn)(不與A. B重合),作∠DMN=60,交∠DBA外角平分線于點(diǎn)N.

(1)求證:DM=MN;
(2)若點(diǎn)M在AB的延長線上,其余條件不變,結(jié)論“DM=MN”是否依然成立?請你畫出圖形并證明你的結(jié)論.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形ABCD中,點(diǎn)E,F分別在邊,AD,CD上,且![]() ,BD和EF交于點(diǎn)O,延長BD至點(diǎn)H,使得
,BD和EF交于點(diǎn)O,延長BD至點(diǎn)H,使得![]() ,并連接HE,HF.
,并連接HE,HF.
![]() 求證:
求證:![]() ;
;
![]() 試判斷四邊形BEHF是什么特殊的四邊形,并說明理由.
試判斷四邊形BEHF是什么特殊的四邊形,并說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商店購進(jìn)![]() 、
、![]() 兩種商品,購買1個(gè)
兩種商品,購買1個(gè)![]() 商品比購買1個(gè)
商品比購買1個(gè)![]() 商品多花10元,并且花費(fèi)300元購買
商品多花10元,并且花費(fèi)300元購買![]() 商品和花費(fèi)100元購買
商品和花費(fèi)100元購買![]() 商品的數(shù)量相等.
商品的數(shù)量相等.
(1)求購買一個(gè)![]() 商品和一個(gè)
商品和一個(gè)![]() 商品各需要多少元;
商品各需要多少元;
(2)商店準(zhǔn)備購買![]() 、
、![]() 兩種商品共80個(gè),若
兩種商品共80個(gè),若![]() 商品的數(shù)量不少于
商品的數(shù)量不少于![]() 商品數(shù)量的4倍,并且購買
商品數(shù)量的4倍,并且購買![]() 、
、![]() 商品的總費(fèi)用不低于1000元且不高于1050元,那么商店有哪幾種購買方案?
商品的總費(fèi)用不低于1000元且不高于1050元,那么商店有哪幾種購買方案?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】三臺縣某中學(xué)“五![]() 四”青年節(jié)舉行了“班班有歌聲”歌詠比賽活動(dòng)
四”青年節(jié)舉行了“班班有歌聲”歌詠比賽活動(dòng)![]() 比賽聘請了10位教師和10位學(xué)生擔(dān)任評委,其中甲班的得分情況如統(tǒng)計(jì)表和統(tǒng)計(jì)圖.
比賽聘請了10位教師和10位學(xué)生擔(dān)任評委,其中甲班的得分情況如統(tǒng)計(jì)表和統(tǒng)計(jì)圖.
老師評委評分統(tǒng)計(jì)表:
評委序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
分?jǐn)?shù) | 94 | 96 | 93 | 91 | x | 92 | 91 | 98 | 96 | 93 |
學(xué)生評委評分折線統(tǒng)計(jì)圖師生評委評分頻數(shù)分布直方圖

![]() 補(bǔ)全頻數(shù)分布直方圖.
補(bǔ)全頻數(shù)分布直方圖.
![]() 學(xué)生評委評分的中位數(shù)是______.
學(xué)生評委評分的中位數(shù)是______.
![]() 計(jì)分辦法規(guī)定:老師評委、學(xué)生評委的評分各去掉一個(gè)最高分、一個(gè)最低分,并且按教師、學(xué)生各占
計(jì)分辦法規(guī)定:老師評委、學(xué)生評委的評分各去掉一個(gè)最高分、一個(gè)最低分,并且按教師、學(xué)生各占![]() 、
、![]() 的方法計(jì)算各班最后得分,知甲班最后得分
的方法計(jì)算各班最后得分,知甲班最后得分![]() 分,試求統(tǒng)計(jì)表中的x.
分,試求統(tǒng)計(jì)表中的x.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下列材料,解答下面的問題:
我們知道方程![]() 有無數(shù)個(gè)解,但在實(shí)際問題中往往只需求出其正整數(shù)解.
有無數(shù)個(gè)解,但在實(shí)際問題中往往只需求出其正整數(shù)解.
例:由![]() ,得:
,得:![]() (
( ![]() 、
、![]() 為正整數(shù)).要使
為正整數(shù)).要使![]() 為正整數(shù),則
為正整數(shù),則![]() 為正整數(shù),可知:
為正整數(shù),可知: ![]() 為3的倍數(shù),從而
為3的倍數(shù),從而![]() ,代入
,代入![]() .所以
.所以![]() 的正整數(shù)解為
的正整數(shù)解為![]() .
.
問題:
(1)請你直接寫出方程![]() =8的正整數(shù)解 .
=8的正整數(shù)解 .
(2)若![]() 為自然數(shù),則滿足條件的正整數(shù)
為自然數(shù),則滿足條件的正整數(shù)![]() 的值有( )
的值有( )
A.3個(gè) B.4個(gè) C.5個(gè) D.6個(gè)
(3)關(guān)于![]() ,
, ![]() 的二元一次方程組
的二元一次方程組![]() 的解是正整數(shù),求整數(shù)
的解是正整數(shù),求整數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,∠CAB=30°.以AB長為一邊作△ABD,且AD=BD,∠ADB=90°,取AB中點(diǎn)E,連DE、CE、CD.則∠EDC是多少度.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在等邊三角形ABC中,點(diǎn)P在△ABC內(nèi),點(diǎn)Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
(1)求證:△ABP≌△ACQ;
(2)請判斷△APQ是什么三角形,試說明你的結(jié)論.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() 分別交x軸、y軸于A、B兩點(diǎn),拋物線
分別交x軸、y軸于A、B兩點(diǎn),拋物線![]() 經(jīng)過點(diǎn)A,和x軸的另一個(gè)交點(diǎn)為C.
經(jīng)過點(diǎn)A,和x軸的另一個(gè)交點(diǎn)為C.

![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 如圖1,點(diǎn)D是拋物線上的動(dòng)點(diǎn),且在第三象限,求
如圖1,點(diǎn)D是拋物線上的動(dòng)點(diǎn),且在第三象限,求![]() 面積的最大值;
面積的最大值;
![]() 如圖2,經(jīng)過點(diǎn)
如圖2,經(jīng)過點(diǎn)![]() 的直線交拋物線于點(diǎn)P、Q,連接CP、CQ分別交y軸于點(diǎn)E、F,求
的直線交拋物線于點(diǎn)P、Q,連接CP、CQ分別交y軸于點(diǎn)E、F,求![]() 的值.
的值.
備注:拋物線頂點(diǎn)坐標(biāo)公式![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com