
【題目】已知:如圖,二次函數y=ax2+bx+c的圖象與x軸交于A、B兩點,其中A點坐標為(﹣1,0),點C(0,5),另拋物線經過點(1,8),M為它的頂點.
(1)求拋物線的解析式;
(2)求△MCB的面積![]() .
.
(3)在坐標軸上,是否存在點N,滿足△BCN為直角三角形?如存在,請直接寫出所有滿足條件的點N.
【答案】(1)y=﹣x2+4x+5(2)15(3)存在,(0,0)或(0,﹣5)或(﹣5,0)
【解析】
試題分析:(1)把A(﹣1,0),C(0,5),(1,8)三點代入二次函數解析式,解方程組即可.
(2)先求出M、B、C的坐標,根據![]() 即可解決問題.
即可解決問題.
(3)分三種情①C為直角頂點;②B為直角頂點;③N為直角頂點;分別求解即可.
試題解析:(1)∵二次函數y=ax2+bx+c的圖象經過A(﹣1,0),C(0,5),(1,8),
則有: ,
,
解得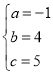 .
.
∴拋物線的解析式為y=﹣x2+4x+5.
(2)令y=0,得(x﹣5)(x+1)=0,x1=5,x2=﹣1,
∴B(5,0).
由y=﹣x2+4x+5=﹣(x﹣2)2+9,得頂點M(2,9)
如圖1中,作ME⊥y軸于點E,
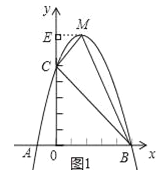
可得![]() =
=![]() (2+5)×9﹣
(2+5)×9﹣![]() ×4×2﹣
×4×2﹣![]() ×5×5=15.
×5×5=15.
(3)存在.如圖2中,
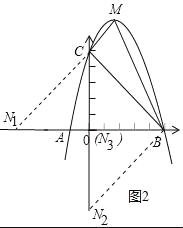
∵OC=OB=5,
∴△BOC是等腰直角三角形,
①當C為直角頂點時,N1(﹣5,0).
②當B為直角頂點時,N2(0,﹣5).
③當N為直角頂點時,N3(0,0).
綜上所述,滿足條件的點N坐標為(0,0)或(0,﹣5)或(﹣5,0).


科目:初中數學 來源: 題型:
【題目】若一個三角形三邊a,b,c滿足(a+b)2=c2+2ab,則這個三角形是( )
A. 等邊三角形 B. 鈍角三角形 C. 等腰直角三角形 D. 直角三角形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AOB=90°,∠AOC為∠AOB外的一個銳角,且∠AOC=30°,射線OM平分∠BOC,ON平分∠AOC. 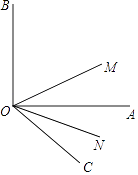
(1)求∠MON的度數;
(2)如果(1)中∠AOB=α,其他條件不變,求∠MON的度數;
(3)如果(1)中∠AOC=β(β為銳角),其他條件不變,求∠MON的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,墻面OC與地面OD垂直,一架梯子AB長5米,開始時梯子緊貼墻面,梯子頂端A沿墻面勻速每分鐘向下滑動1米,x分鐘后點A滑動到點A′,梯子底端B沿地面向左滑動到點B′,OB′=y米,滑動時梯子長度保持不變.
(1)當x=1時,y= 米;
(2)求y關于x的函數關系式,并寫出自變量x的取值范圍;
(3)研究(2)中函數圖象及其性質.
①填寫下表,并在所給的坐標系中畫出函數圖象;
②如果點P(x,y)在(2)中的函數圖象上,求證:點P到點Q(5,0)的距離是定值;
(4)梯子底端B沿地面向左滑動的速度是
A.勻速 B.加速 C.減速 D.先減速后加速.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據圖1,圖2所提供的信息,解答下列問題:
(1)2007年海南省城鎮居民人均可支配收入為 元,比2006年增長 %;
(2)求2008年海南省城鎮居民人均可支配收入(精確到1元),并補全條形統計圖;
(3)根據圖1指出:2005﹣2008年海南省城鎮居民人均可支配收入逐年 (填“增加”或“減少”).

查看答案和解析>>
科目:初中數學 來源: 題型:
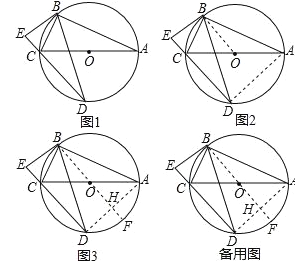
【題目】問題呈現:
如圖1,⊙O是Rt△ABC的外接圓,∠ABC=90°,弦BD=BA,BE⊥DC交DC的延長線于點E.求證:BE是⊙O的切線.
問題分析:
連接OB,要證明BE是⊙O的切線,只要證明OB ____ BE,由題意知∠E=90°,故只需證明OB ___ DE.
解法探究:
(1)小明對這個問題進行了如下探索,請補全他的證明思路:
如圖2,連接AD,由∠ECB是圓內接四邊形ABCD的一個外角,可證∠ECB=∠BAD,因為OB=OC,所以 __ ,因為BD=BA,所以 ______ ,利用同弧所對的圓周角相等和等量代換,得到 ____ ,所以DE∥OB,從而證明出BE是⊙O的切線.
(2)如圖3,連接AD,作直徑BF交AD于點H,小麗發現BF⊥AD,請說明理由.
(3)利用小麗的發現,請證明BE是⊙O的切線.(要求給出兩種不同的證明方法).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com