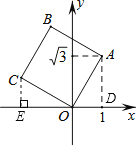
【題目】如圖，將正方形OABC放在平面直角坐標系中，O是原點，A的坐標為（1，
），則點C的坐標為（ ）
A. （
，－1）B. （－1，）C. （，1）D. （－，1）
【答案】D
【解析】
過點A作AD⊥x軸于D，過點C作CE⊥x軸于E，根據同角的余角相等求出∠OAD=∠COE，再利用“角角邊”證明△AOD和△OCE全等，根據全等三角形對應邊相等可得OE=AD，CE=OD，然后根據點C在第二象限寫出坐標即可．
如圖，過點A作AD⊥x軸于D，過點C作CE⊥x軸于E，
∵四邊形OABC是正方形，
∴OA=OC，∠AOC=90°，
∴∠COE+∠AOD=90°，
又∵∠OAD+∠AOD=90°，
∴∠OAD=∠COE，
在△AOD和△OCE中，
，
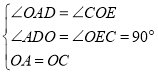∴△AOD≌△OCE（AAS），
∴OE=AD=
，CE=OD=1，
∵點C在第二象限，
∴點C的坐標為（-，1）．
故選：D．
科目：初中數學 來源： 題型：
【題目】如圖，在單位為1的方格紙上，△A1A2A3，△A3A4A5，△A5A6A7，…，都是斜邊在x軸上，斜邊長分別為2，4，6，…的等直角三角形，若△A1A2A3的頂點坐標分別為A1（2，0），A2（1，1），A3（0，0），則依圖中所示規律，A2019的坐標為（ ）
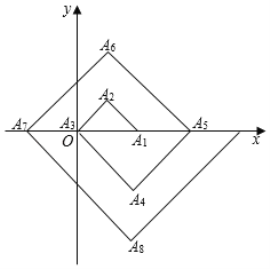
A.（﹣1008，0）B.（﹣1006，0）C.（2，﹣504）D.（1，505）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某通訊運營商的手機上網流量資費標準推出了三種優惠方案：
方案A:按流量計費，0.1元/M；
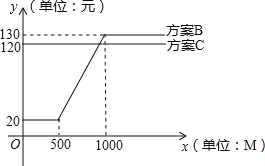
方案B:20元流量套餐包月，包含500M流量，如果超過500M，超過部分另外計費（見圖象），如果用到1000M時，超過1000M的流量不再收費；
方案C:120元包月，無限制使用.
用x表示每月上網流量(單位：M),y表示每月的流量費用(單位：元)，方案B和方案C對應的y關于x的函數圖象如圖所示，請解決以下問題：
(1)寫出方案A的函數解析式，并在圖中畫出其圖象；
(2)直接寫出方案B的函數解析式；
(3)若甲乙兩人每月使用流量分別在300—600M，800—1200M之間，請你分別給出甲乙二人經濟合理的選擇方案.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】發現
如圖1，在有一個“凹角∠A1A2A3”n邊形A1A2A3A4……An中（n為大于3的整數），∠A1A2A3＝∠A1+∠A3+∠A4+∠A5+∠A6+……+∠An﹣（n﹣4）×180°．
驗證
（1）如圖2，在有一個“凹角∠ABC”的四邊形ABCD中，證明：∠ABC＝∠A+∠C+∠D．
（2）證明3，在有一個“凹角∠ABC”的六邊形ABCDEF中，證明；∠ABC＝∠A+∠C+∠D+∠E+∠F﹣360°．
延伸
（3）如圖4，在有兩個連續“凹角A1A2A3和∠A2A3A4”的四邊形A1A2A3A4……An中（n為大于4的整數），∠A1A2A3+∠A2A3A4＝∠A1+∠A4+∠A5+∠A6……+∠An﹣（n﹣ ）×180°．
查看答案和解析>>
科目：初中數學 來源： 題型：
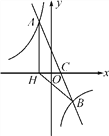
【題目】如圖，在平面直角坐標系中，一次函數y＝ax＋b(a≠0)的圖象與反比例函數y＝
(k≠0)的圖象交于A，B兩點，與x軸交于點C，過點A作AH⊥x軸于點H，點O是線段CH的中點，AC＝4 
，cos∠ACH＝
，點B的坐標為(4，n)．
(1)求該反比例函數和一次函數的解析式；
(2)求△BCH的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如果一個三角形能被一條線段分割成兩個等腰三角形，那么稱這條線段為這個三角形的特異線，稱這個三角形為特異三角形．
（1）如圖1，△ABC是等腰銳角三角形，AB=AC(
)，若∠ABC的角平分線BD交AC于點D，且BD是△ABC的一條特異線，則∠BDC=______度；
（2）如圖2，△ABC中，∠B=2∠C，線段AC的垂直平分線交AC于點D，交BC于點E．求證：AE是△ABC的一條特異線；
（3）如圖3，已知△ABC是特異三角形，且∠A=30°，∠B為鈍角，求出所有可能的∠B的度數（如有需要，可在答題卡相應位置另外畫圖）．
查看答案和解析>>
科目：初中數學 來源： 題型：
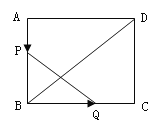
【題目】如圖，已知矩形
，長
，寬
， 
、
分別是
、
上運動的兩點。若
自點
出發，以
的速度沿
方向運動，同時， 
自點
出發以
的速度沿
方向運動，則經過____________秒，以
、
、
為頂點的三角形與
相似。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知點D在△ABC的BC邊上，DE∥AC交AB于E，DF∥AB交AC于F．
（1）求證：AE=DF；
（2）若AD平分∠BAC，試判斷四邊形AEDF的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知一次函數
（k≠0）的圖象經過
， 
兩點，二次函數
（其中a＞2）.
（1）求一次函數的表達式及二次函數圖象的頂點坐標（用含a的代數式表示）；
（2）利用函數圖象解決下列問題：
①若
，求當
且
≤0時，自變量x的取值范圍；
②如果滿足
且
≤0時的自變量x的取值范圍內恰有一個整數，直接寫出a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com