
【題目】已知:如圖①,BP、CP分別平分△ABC的外角∠CBD、∠BCE,BQ、CQ分別平分∠PBC、∠PCB,BM、CN分別是∠PBD、∠PCE的角平分線.
(1)當∠BAC=40°時,∠BPC= ,∠BQC= ;
(2)當BM∥CN時,求∠BAC的度數;
(3)如圖②,當∠BAC=120°時,BM、CN所在直線交于點O,直接寫出∠BOC的度數.
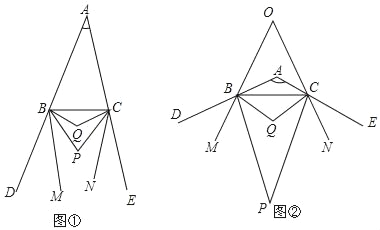
【答案】(1) 70°,125°;(2) ∠BAC=60° (3) 45°
【解析】
(1)根據三角形的外角性質分別表示出∠DBC與∠BCE,再根據角平分線的性質可求得∠CBP+∠BCP,最后根據三角形內角和定理即可求解;根據角平分線的定義得出∠QBC=![]() ∠PBC,∠QCB=
∠PBC,∠QCB=![]() ∠PCB,求出∠QBC+∠QCB的度數,根據三角形內角和定理求出即可;
∠PCB,求出∠QBC+∠QCB的度數,根據三角形內角和定理求出即可;
(2)根據平行線的性質得到∠MBC+∠NCB=180°,依此求解即可;
(3)根據題意得到∠MBC+∠NCB,再根據三角形外角的性質和三角形內角和定理得到∠BOC的度數.
(1)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=180°+∠A=220°,
∵BP、CP分別是△ABC的外角∠CBD、∠BCE的角平分線,
∴∠CBP+∠BCP=![]() (∠DBC+∠BCE)=110°,
(∠DBC+∠BCE)=110°,
∴∠BPC=180°﹣110°=70°,
∵BQ、CQ分別是∠PBC、∠PCB的角平分線,
∴∠QBC=![]() ∠PBC,∠QCB=
∠PBC,∠QCB=![]() ∠PCB,
∠PCB,
∴∠QBC+∠QCB=55°,
∴∠BQC=180°﹣55°=125°;
(2)∵BM∥CN,
∴∠MBC+∠NCB=180°,
∵BM、CN分別是∠PBD、∠PCE的角平分線,
∴![]() (∠DBC+∠BCE)=180°,
(∠DBC+∠BCE)=180°,
即![]() (180°+∠BAC)=180°,
(180°+∠BAC)=180°,
解得∠BAC=60°;
(3)∵∠BAC=120°,
∴∠MBC+∠NCB=![]() (∠DBC+∠BCE)=
(∠DBC+∠BCE)=![]() (180°+α)=225°,
(180°+α)=225°,
∴∠BOC=225°﹣180°=45°.


科目:初中數學 來源: 題型:
【題目】宜賓是國家級歷史文化名城,大觀樓是標志性建筑之一(如圖①).喜愛數學實踐活動的小偉查資料得知:大觀樓始建于明代(一說是唐代韋皋所建),后毀于兵火,乾隆乙酉年(1765年)重建,它是我國目前現存最高大、最古老的樓閣之一.小偉決定用自己所學習的知識測量大觀樓的高度.如圖②,他利用測角儀站在B處測得大觀樓最高點P的仰角為45°,又前進了12米到達A處,在A處測得P的仰角為60°.請你幫助小偉算算大觀樓的高度.(測角儀高度忽略不計, ![]() ≈1.7,結果保留整數).
≈1.7,結果保留整數).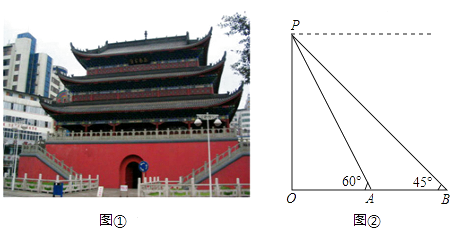
查看答案和解析>>
科目:初中數學 來源: 題型:
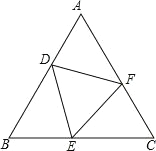
【題目】如圖,△ABC 中,AB=AC,D、E、F 分別為 AB、BC、AC 上的點,且BD=CE,∠DEF=∠B.
(1)求證:∠BDE=∠CEF;
(2)當∠A=60°時,求證:△DEF 為等邊三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場銷售A,B兩種品牌的教學設備,這兩種教學設備的進價和售價如下表所示:
A | B | |
進價(萬元/套) | 1.5 | 1.2 |
售價(萬元/套) | 1.65 | 1.4 |
該商場計劃購進兩種教學設備若干套,共需66萬元,全部銷售后可獲毛利潤9萬元。
(毛利潤=(售價 - 進價)×銷售量)
(1)該商場計劃購進A,B兩種品牌的教學設備各多少套?
(2)通過市場調研,該商場決定在原計劃的基礎上,減少A種設備的購進數量,增加B種設備的購進數量,已知B種設備增加的數量是A種設備減少數量的1.5倍。若用于購進這兩種教學設備的總資金不超過69萬元,問A種設備購進數量至多減少多少套?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在兩建筑物之間有一旗桿,高15米,從A點經過旗桿頂點恰好看到矮建筑物的墻角C點,且俯角α為60°,又從A點測得D點的俯角β為30°,若旗桿底點G為BC的中點,則矮建筑物的高CD為( )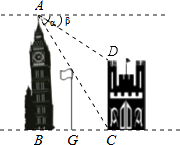
A.20米
B.10 ![]() 米
米
C.15 ![]() 米
米
D.5 ![]() 米
米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,將一塊等腰直角三角板ABC放在第一象限,斜靠在兩條坐標軸上,∠ACB=900,且A(0,4),點C(2,0),BE⊥x軸于點E,一次函數y=x+b經過點B,交y軸于點D。
(1)求證;△AOC≌△CEB
(2)求△ABD的面積。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用直尺和圓規畫一個角等于已知角,是運用了“全等三角形的對應角相等”這一性質,其全等的依據是( )
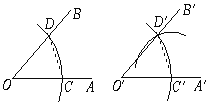
A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在圖①中的正方形中剪去一個邊長為2a+b的正方形,將剩余的部分按圖②的方式拼成一個長方形.
(1)求剪去正方形的面積;
(2)求拼成的長方形的長、寬以及它的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為8,在各邊上順次截取AE=BF=CG=DH=5,則四邊形EFGH的面積是( ) 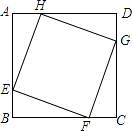
A.30
B.34
C.36
D.40
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com