
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC= ![]() ,BC=3,△DEF是邊長為a(a為小于3的常數)的等邊三角形,將△DEF沿AC方向平移,使點D在線段AC上,DE∥AB,設△DEF與△ABC重疊部分的周長為T.
,BC=3,△DEF是邊長為a(a為小于3的常數)的等邊三角形,將△DEF沿AC方向平移,使點D在線段AC上,DE∥AB,設△DEF與△ABC重疊部分的周長為T.
(1)求證:點E到AC的距離為一個常數;
(2)若AD= ![]() ,當a=2時,求T的值;
,當a=2時,求T的值;
(3)若點D運動到AC的中點處,請用含a的代數式表示T.
【答案】
(1)
解:由題意得:tanA= ![]() =
= ![]() =
= ![]() ,
,
∴∠A=60°.
∵DE∥AB,
∴∠CDE=∠A=60°.
如答圖1所示,過點E作EH⊥AC于點H,

則EH=DEsin∠CDE=a ![]() =
= ![]() a.
a.
∴點E到AC的距離為一個常數
(2)
解:若AD= ![]() ,當a=2時,如答圖2所示.
,當a=2時,如答圖2所示.
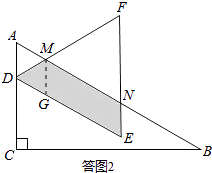
設AB與DF、EF分別交于點M、N.
∵△DEF為等邊三角形,∴∠MDE=60°,
由(1)知∠CDE=60°,
∴∠ADM=180°﹣∠MDE﹣∠CDE=60°,
又∵∠A=60°,
∴△ADM為等邊三角形,
∴DM=AD= ![]() .
.
過點M作MG∥AC,交DE于點G,則∠DMG=∠ADM=60°,
∴△DMG為等邊三角形,
∴DG=MG=DM= ![]() .
.
∴GE=DE﹣DG=2﹣ ![]() =
= ![]() .
.
∵∠MGD=∠E=60°,∴MG∥NE,
又∵DE∥AB,
∴四邊形MGEN為平行四邊形.
∴NE=MG= ![]() ,MN=GE=
,MN=GE= ![]() .
.
∴T=DE+DM+MN+NE=2+ ![]() +
+ ![]() +
+ ![]() =
= ![]()
(3)
解:若點D運動到AC的中點處,分情況討論如下:
①若0<a≤ ![]() ,△DEF在△ABC內部,如答圖3所示:
,△DEF在△ABC內部,如答圖3所示:

∴T=3a;
②若 ![]() <a≤
<a≤ ![]() ,點E在△ABC內部,點F在△ABC外部,在如答圖4所示:
,點E在△ABC內部,點F在△ABC外部,在如答圖4所示:

設AB與DF、EF分別交于點M、N,過點M作MG∥AC交DE于點G.
與(2)同理,可知△ADM、△DMG均為等邊三角形,四邊形MGEN為平行四邊形.
∴DM=DG=NE=AD= ![]() ,MN=GE=DE﹣DG=a﹣
,MN=GE=DE﹣DG=a﹣ ![]() ,
,
∴T=DE+DM+MN+NE=a+ ![]() +(a﹣
+(a﹣ ![]() )+
)+ ![]() =2a+
=2a+ ![]() ;
;
③若 ![]() <a<3,點E、F均在△ABC外部,如答圖5所示:
<a<3,點E、F均在△ABC外部,如答圖5所示:

設AB與DF、EF分別交于點M、N,BC與DE、EF分別交于點P、Q.
在Rt△PCD中,CD= ![]() ,∠CDP=60°,∠DPC=30°,
,∠CDP=60°,∠DPC=30°,
∴PC=CDtan60°= ![]() ×
× ![]() =
= ![]() .
.
∵∠EPQ=∠DPC=30°,∠E=60°,∴∠PQE=90°.
由(1)知,點E到AC的距離為 ![]() a,∴PQ=
a,∴PQ= ![]() a﹣
a﹣ ![]() .
.
∴QE=PQtan30°=( ![]() a﹣
a﹣ ![]() )×
)× ![]() =
= ![]() a﹣
a﹣ ![]() ,PE=2QE=a﹣
,PE=2QE=a﹣ ![]() .
.
由②可知,四邊形MDEN的周長為2a+ ![]() .
.
∴T=四邊形MDEN的周長﹣PE﹣QE+PQ=(2a+ ![]() )﹣(a﹣
)﹣(a﹣ ![]() )﹣(
)﹣( ![]() a﹣
a﹣ ![]() )+(
)+( ![]() a﹣
a﹣ ![]() )=
)= ![]() a+
a+ ![]() ﹣
﹣ ![]() .
.
綜上所述,若點D運動到AC的中點處,T的關系式為:
T= 
【解析】(1)解直角三角形,求得點E到AC的距離等于 ![]() a,這是一個定值;(2)如答圖2所示,作輔助線,將四邊形MDEN分成一個等邊三角形和一個平行四邊形,求出其周長;(3)可能存在三種情形,需要分類討論:①若0<a≤
a,這是一個定值;(2)如答圖2所示,作輔助線,將四邊形MDEN分成一個等邊三角形和一個平行四邊形,求出其周長;(3)可能存在三種情形,需要分類討論:①若0<a≤ ![]() ,△DEF在△ABC內部,如答圖3所示;②若
,△DEF在△ABC內部,如答圖3所示;②若 ![]() <a≤
<a≤ ![]() ,點E在△ABC內部,點F在△ABC外部,在如答圖4所示;③若
,點E在△ABC內部,點F在△ABC外部,在如答圖4所示;③若 ![]() <a<3,點E、F均在△ABC外部,如答圖5所示.
<a<3,點E、F均在△ABC外部,如答圖5所示.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,一次函數y1=k1x+b與反比例函數 ![]() 的圖象相交于A,B兩點,且與坐標軸的交點為(﹣6,0),(0,6),點B的橫坐標為﹣4.
的圖象相交于A,B兩點,且與坐標軸的交點為(﹣6,0),(0,6),點B的橫坐標為﹣4. 
(1)試確定反比例函數的解析式;
(2)求△AOB的面積;
(3)直接寫出不等式 ![]() 的解.
的解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,點P在邊CD上,且與C、D不重合,過點A作AP的垂線與CB的延長線相交于點Q,連接PQ,M為PQ中點.
(1)求證:△ADP∽△ABQ;
(2)若AD=10,AB=20,點P在邊CD上運動,設DP=x,BM2=y,求y與x的函數關系式,并求線段BM的最小值;
(3)若AD=10,AB=a,DP=8,隨著a的大小的變化,點M的位置也在變化.當點M落在矩形ABCD外部時,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小李與小陸從A地出發(fā),騎自行車沿同一條路行駛到B地,他們離出發(fā)地的距離S(單位:km)和行駛時間t(單位:h)之間的函數關系的圖象如圖所示,根據圖中提供的信息,有下列說法: 1)他們都行駛了20km;
2)小陸全程共用了1.5h;
3)小李與小陸相遇后,小李的速度小于小陸的速度;
4)小李在途中停留了0.5h.
其中正確的有( )
A.4個
B.3個
C.2個
D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果批發(fā)市場將一批蘋果分為A,B,C,D四個等級,統(tǒng)計后將結果制成條形圖,已知A等級蘋果的重量占這批蘋果總重量的30%. 回答下列問題: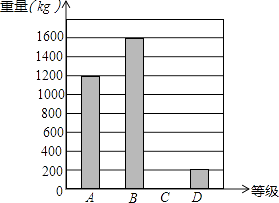
(1)這批蘋果總重量為kg;
(2)請將條形圖補充完整;
(3)若用扇形圖表示統(tǒng)計結果,則C等級蘋果所對應扇形的圓心角為度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=a(x﹣m)2﹣a(x﹣m)(a,m為常數,且a≠0).
(1)求證:不論a與m為何值,該函數的圖象與x軸總有兩個公共點.
(2)設該函數的圖象的頂點為C,與x軸交于A,B兩點,與y軸交于D點.
①當△ABC的面積為1時,求a的值.
②當△ABC的面積與△ABD的面積相等時,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y1=﹣x2+mx+n,直線y2=kx+b,y1的對稱軸與y2交于點A(﹣1,5),點A與y1的頂點B的距離是4.
(1)求y1的解析式;
(2)若y2隨著x的增大而增大,且y1與y2都經過x軸上的同一點,求y2的解析式.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com