
 分別交x軸、y軸點A、B,⊙O的半徑為
分別交x軸、y軸點A、B,⊙O的半徑為 個單位長度.點P為直線
個單位長度.點P為直線 上的動點,過點P作⊙O的切線PC、PD ,切點分別為C、D,且PC⊥PD.
上的動點,過點P作⊙O的切線PC、PD ,切點分別為C、D,且PC⊥PD.
 將⊙O的圓周分成兩段弧長之比為1∶3,請直接寫出b的值:b= .
將⊙O的圓周分成兩段弧長之比為1∶3,請直接寫出b的值:b= .
 或-
或-
 與x軸、y軸的交點坐標即可得到結果;
與x軸、y軸的交點坐標即可得到結果; 將圓周分成兩段弧長之比為1∶3,可知被割得的弦所對的圓心角為90
將圓周分成兩段弧長之比為1∶3,可知被割得的弦所對的圓心角為90 ,又直線
,又直線 與坐標軸的夾角為45
與坐標軸的夾角為45 ,即可求得結果.
,即可求得結果. 中,當x=0時,y=4,當y=0時,x=4
中,當x=0時,y=4,當y=0時,x=4
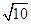 )2,
)2,
 將圓周分成兩段弧長之比為1∶3,可知被割得的弦所對的圓心角為90
將圓周分成兩段弧長之比為1∶3,可知被割得的弦所對的圓心角為90 ,又直線
,又直線 與坐標軸的夾角為45
與坐標軸的夾角為45 ,如圖可知,分兩種情況,所以,b的值為
,如圖可知,分兩種情況,所以,b的值為 或-
或- .
. 


科目:初中數學 來源:不詳 題型:單選題
| A.(-2,0) | B.(2,0) |
| C.(4,0) | D.(0,0) |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 經過點A(0,5),B(1,4).
經過點A(0,5),B(1,4).
 與直線AB相交于點C,求點C的坐標;
與直線AB相交于點C,求點C的坐標;查看答案和解析>>
科目:初中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

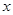 噸,請寫出將糧食運往A、B兩庫的總運費
噸,請寫出將糧食運往A、B兩庫的總運費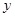 (元)與
(元)與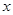 (噸)的函數關系式;
(噸)的函數關系式;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com