
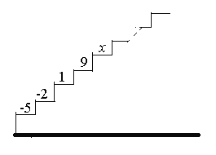
【題目】如圖,階梯圖的每個臺階上都標著一個數,從下到上的第1個至第4個臺階上依次標著-5,-2,1,9,且任意相鄰四個臺階上數的和都相等.
(1)求前4個臺階上數的和是多少?
(2)求第5個臺階上的數![]() 是多少?
是多少?
(3)從下到上前多少個臺階上數的和為30.
【答案】(1)3;(2)-5;(3)40或51
【解析】
(1)把錢4個臺階上的數字相加即可;(2)根據任意相鄰四個臺階上數的和都相等,把第2個臺階至第5個臺階上的數字相加所得的和與(1)中的結果相等,解方程求得x即可;(3)通過(1)(2)的計算,可知臺階上的數字四個一循環,并且4個數字的和為3,①30÷3=10,可知10個循環后所有數字的和為30,此時共有40個臺階;②36+(-5)+(-2)+1=30,36÷3=12,可知第12個循環后所有數字的和加上第13個循環的前3個數的和為30,此時共有12×4+3=51個臺階.由此即可解答.
(1)-5+(-2)+1+9=3.
∴前4個臺階上數的和是3.
(2)由題意得,-2+1+9+x=3,
解得x=-5.
∴第5個臺階上的數x是-5.
(3)通過(1)(2)的計算,可知臺階上的數字四個一循環,并且4個數字的和為3,
①30÷3=10,可知10個循環后所有數字的和為30,此時共有40個臺階;
②36+(-5)+(-2)+1=30,36÷3=12,可知第12個循環后所有數字的和加上第13個循環的前3個數的和為30,此時共有12×4+3=51個臺階.
∴從下到上前40個或51個臺階上數的和為30.


 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,用火柴棒按下列方式搭三角形:

(1)填寫下面表
三角形個數 | 1 | 2 | 3 | 4 | … |
火柴棒根數 | … |
(2)搭10個這樣的三角形需要 根火柴棒.
(3)搭n個這樣的三角形需要 根火柴棒.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,AB是⊙O的直徑,點C在⊙O上,過點C的直線與AB的延長線交于點P. 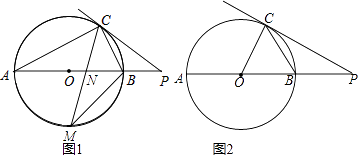
(1)如圖①,若∠COB=2∠PCB,求證:直線PC是⊙O的切線;
(2)如圖②,若點M是AB的中點,CM交AB于點N,MNMC=36,求BM的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O中,AB是直徑,點D是⊙O上一點,點C是弧AD的中點,弦CE⊥AB于點E,過點D的切線交EC的延長線于點G,連接AD,分別交CE、CB于點P、Q,連接AC,給出下列結論:①∠DAC=∠ABC;②AD=CB;③點P是△ACQ的外心;④AC2=AEAB;⑤CB∥GD,其中正確的結論是( ) 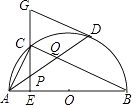
A.①③⑤
B.②④⑤
C.①②⑤
D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCD的四個角向內折起,恰好拼成一個無縫隙無重疊的四邊形EFGH,EH=12厘米,EF=16厘米,則邊AD的長是( )

A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
查看答案和解析>>
科目:初中數學 來源: 題型:
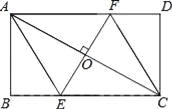
【題目】如圖,AC是矩形ABCD的對角線,過AC的中點O作EF⊥AC,交BC于點E,交AD于點F,連接AE,CF.
(1)求證:四邊形AECF是菱形;
(2)若AB=![]() ,∠DCF=30°,求四邊形AECF的面積.(結果保留根號)
,∠DCF=30°,求四邊形AECF的面積.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,E是AB上一點,BE=2,AE=3,P是AC上一動點,則PB+PE的最小值是( ).

A. 5 B. 5![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的正方形組成的網格中,△AOB的頂點均在格點上,點A、B的坐標分別是A(3,2),B(1,3),△AOB繞點O逆時針旋轉90°后得到△A1OB1 . 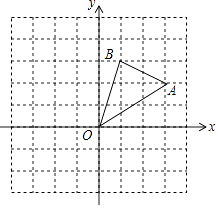
(1)點A關于點O中心對稱的點P的坐標為;
(2)在網格內畫出△A1OB1;
(3)點A1、B1的坐標分別為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,分別以Rt△ABC的直角邊AC及斜邊AB向外作等邊△ACD及等邊△ABE.已知∠BAC=30°,EF⊥AB,垂足為F,連接DF.

(1)試說明AC=EF;
(2)求證:四邊形ADFE是平行四邊形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com