
【題目】如圖,AD是△ABC的角平分線,以AD為弦的⊙O交AB、AC于E、F,已知EF∥BC.
(1)求證:BC是⊙O的切線;
(2)若已知AE=12,CF=6,求DE的長.
【答案】
(1)
證明:連接OD,
∵AD是△ABC的角平分線,
∴∠1=∠2,
∴ ![]() =
= ![]() ,
,
∴OD⊥EF,
∵EF∥BC,
∴OD⊥BC,
∴BC是⊙O的切線;
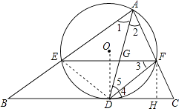
(2)
解:連接DE,
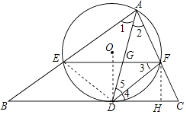
∵ ![]() =
= ![]() ,
,
∴DE=DF,
∵EF∥BC,
∴∠3=∠4,
∵∠1=∠3,
∴∠1=∠4,
∵∠DFC=∠AED,
∴△AED∽△DFC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴DE2=72,
∴DE=6 ![]() .
.
【解析】(1)連接OD,由角平分線的定義得到∠1=∠2,得到 ![]() =
= ![]() ,根據垂徑定理得到OD⊥EF,根據平行線的性質得到OD⊥BC,于是得到結論;(2)連接DE,由
,根據垂徑定理得到OD⊥EF,根據平行線的性質得到OD⊥BC,于是得到結論;(2)連接DE,由 ![]() =
= ![]() ,得到DE=DF,根據平行線的性質得到∠3=∠4,等量代換得到∠1=∠4,根據相似三角形的性質即可得到結論;
,得到DE=DF,根據平行線的性質得到∠3=∠4,等量代換得到∠1=∠4,根據相似三角形的性質即可得到結論;


科目:初中數學 來源: 題型:
【題目】已知,A點的坐標為(4,3),過A點分別作坐標軸的垂線,交x軸和y軸分別于B點和C點,P為線段AB上一個動點(P不與A,B重合),過點P的反比例函數y= ![]() 的圖象與AC交于點D.
的圖象與AC交于點D.

(1)當△PBC的面積等于4時,求該反比例函數的解析式;
(2)當k為何值時,△PBD的面積最大,最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某市初三學生的體育測試成績和課外體育鍛煉時間的情況,現從全市初三學生體育測試成績中隨機抽取200名學生的體育測試成績作為樣本.體育成績分為四個等次:優秀、良好、及格、不及格.
體育鍛煉時間 | 人數 |
4≤x≤6 |
|
2≤x<4 | 43 |
0≤x<2 | 15 |

(1)試求樣本扇形圖中體育成績“良好”所對扇形圓心角的度數;
(2)統計樣本中體育成績“優秀”和“良好”學生課外體育鍛煉時間表(如圖表所示),請將圖表填寫完整(記學生課外體育鍛煉時間為x小時);
(3)全市初三學生中有14400人的體育測試成績為“優秀”和“良好”,請估計這些學生中課外體育鍛煉時間不少于4小時的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,矩形OABC的頂點O與坐標原點重合,頂點A,C分別在坐標軸上,頂點B的坐標(4,2),過點D(0,3)和E(6,0)的直線分別于AB,BC交于點M,N. 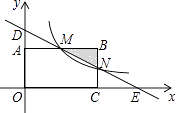
(1)求直線DE的解析式和點M的坐標;
(2)若反比例函數y= ![]() (x>0)的圖象經過點M,求該反比例函數的解析式,并通過計算判斷點N是否在該函數的圖象上.
(x>0)的圖象經過點M,求該反比例函數的解析式,并通過計算判斷點N是否在該函數的圖象上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等腰Rt△ABC中,∠C=90°,AC=8,F是AB邊上的中點,點D、E分別在AC、BC邊上運動,且保持AD=CE.連接DE、DF、EF.在此運動變化的過程中,下列結論:
①△DFE是等腰直角三角形;
②四邊形CDFE不可能為正方形;
③四邊形CDFE的面積保持不變;
④△CDE面積的最大值為8.
其中正確的結論有( )個.
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A(﹣3,1),以點O為頂點作等腰直角三角形AOB,雙曲線y1=![]() 在第一象限內的圖象經過點B.設直線AB的解析式為y2=k2x+b,當y1>y2時,x的取值范圍是( )
在第一象限內的圖象經過點B.設直線AB的解析式為y2=k2x+b,當y1>y2時,x的取值范圍是( )
A.﹣5<x<1
B.0<x<1或x<﹣5
C.﹣6<x<1
D.0<x<1或x<﹣6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,我南海某海域A處有一艘捕魚船在作業時突遇特大風浪,船長馬上向我國漁政搜救中心發出求救信號,此時一艘漁政船正巡航到捕魚船正西方向的B處,該漁政船收到漁政求救中心指令后前去救援,但兩船之間有大片暗礁,無法直線到達,于是決定馬上調整方向,先向北偏東60°方向以每小時30海里的速度航行半小時到達C處,同時捕魚船低速航行到A點的正北1.5海里D處,漁政船航行到點C處時測得點D在南偏東53°方向上.
(參考數據:sin53°≈![]() , cos53°≈
, cos53°≈![]() , tan53°≈
, tan53°≈![]() )
)
(1)求CD兩點的距離;
(2)漁政船決定再次調整航向前去救援,若兩船航速不變,并且在點E處相會合,求∠ECD的正弦值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+![]() 與x軸交于A(﹣3,0),B(1,0)兩點.與y軸交于點C,點D與點C關于拋物線的對稱軸對稱.
與x軸交于A(﹣3,0),B(1,0)兩點.與y軸交于點C,點D與點C關于拋物線的對稱軸對稱.
(1)求拋物線的解析式,并直接寫出點D的坐標;
(2)如圖1,點P從點A出發,以每秒1個單位長度的速度沿A→B勻速運動,到達點B時停止運動.以AP為邊作等邊△APQ(點Q在x軸上方),設點P在運動過程中,△APQ與四邊形AOCD重疊部分的面積為S,點P的運動時間為t秒,求S與t之間的函數關系式;
(3)如圖2,連接AC,在第二象限內存在點M,使得以M、O、A為頂點的三角形與△AOC相似.請直接寫出所有符合條件的點M坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com