
【題目】將一副三角尺如圖拼接:含30°角的三角尺(△ABC)的長直角邊與含45°角的三角尺(△ACD)的斜邊恰好重合.已知AB=2 ![]() ,P是AC上的一個動點.
,P是AC上的一個動點.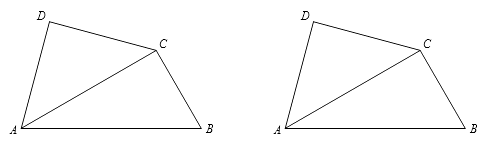
(1)當點P運動到∠ABC的平分線上時,連接DP、BP,求CP、DP的長;
(2)當點P在運動過程中出現PD=BC時,求此時∠PDA的度數;
(3)當點P運動到什么位置時,以D,P,B,Q為頂點的平行四邊形的頂點Q恰好在邊BC上?求出此時平行四邊形的面積.
【答案】
(1)
解:在Rt△ABC中,AB=2![]() ,∠BAC=30°,∴BC=
,∠BAC=30°,∴BC=![]() ,AC=3.
,AC=3.
(1)如圖(1),作DF⊥AC,
∵Rt△ACD中,AD=CD,
∴DF=AF=CF=![]() .
.
∵BP平分∠ABC,
∴∠PBC=30°,
∴CP=1,PF=![]() ,
,
∴DP=![]() =
=![]() .
.

(2)
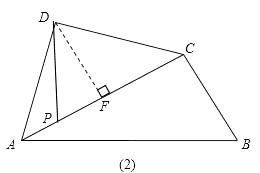
解:當P點位置如圖(2)所示時,
根據(1)中結論,DF=![]() ,∠ADF=45°,又PD=BC=
,∠ADF=45°,又PD=BC=![]() ,
,
∴![]() =
=![]() ,
,
∴∠PDF=30°.
∴∠PDA=∠ADF-∠PDF=15°.
當P點位置如圖(3)所示時,同(2)可得∠PDF=30°.
∴∠PDA=∠ADF+∠PDF=75°.

(3)
解:∵BC⊥AC
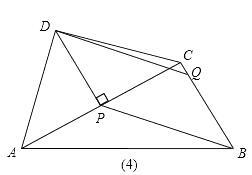
∴只有當DP⊥AC時,以D,P,B,Q為頂點的四邊形為平行四邊形.
如圖,在DPBQ中,BC∥DP,
∵∠ACB=90°,
∴DP⊥AC.
根據(1)中結論可知,DP=CP=![]() ,
,
∴SDPBQ=DP·CP=![]() .
.
【解析】(1)含30度角的直角三角形中,三邊的比是1:![]() :2,依此可求得CP;構造直角三角形PDF,先求出PF和DE,即可求得PD;
:2,依此可求得CP;構造直角三角形PDF,先求出PF和DE,即可求得PD;
(2)分類討論:P在DF左邊和P在DF右邊;
(3)只能是DP//BC,且DP=BC,則DP⊥AC,CP是平行線DP與BC之間的距離,則SDPBQ=DP·CP.


科目:初中數學 來源: 題型:
【題目】如圖,△ABC經過平移后得到△DEF,下列結論:①AB∥DE;②AD=BE;③BC=EF;④∠ACB=∠DFE,其中正確的有( )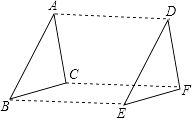
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
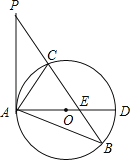
【題目】如圖,已知在△ABP中,C是BP邊上一點,∠PAC=∠PBA,⊙O是△ABC的外接圓,AD是⊙O的直徑,且交BP于點E.
(1)求證:PA是⊙O的切線;
(2)過點C作CF⊥AD,垂足為點F,延長CF交AB于點G,若AGAB=12,求AC的長;
(3)在滿足(2)的條件下,若AF:FD=1:2,GF=1,求⊙O的半徑及sin∠ACE的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
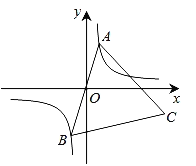
【題目】如圖,已知點A是雙曲線![]() 在第三象限分支上的一個動點,連結AO并延長交另一分支于點B,以AB為邊作等邊三角形ABC,點C在第四象限內,且隨著點A的運動,點C的位置也在不斷變化,但點C始終在雙曲線
在第三象限分支上的一個動點,連結AO并延長交另一分支于點B,以AB為邊作等邊三角形ABC,點C在第四象限內,且隨著點A的運動,點C的位置也在不斷變化,但點C始終在雙曲線![]() 上運動,則k的值是 .
上運動,則k的值是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學完第2章“特殊的三角形”后,老師布置了一道思考題:
如圖,點M、N分別在正三角形ABC的BC,CA邊上,且BM=CN,AM,BN交于點Q.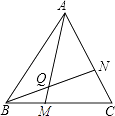
(1)判斷△ABM與△BCN是否全等,并說明理由.
(2)判斷∠BQM是否會等于60°,并說明理由.
(3)若將題中的點M,N分別移動到BC,CA的延長線上,且BM=CN,是否能得到∠BQM=60°?請說明理由. 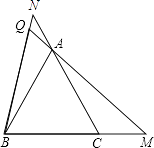
查看答案和解析>>
科目:初中數學 來源: 題型:
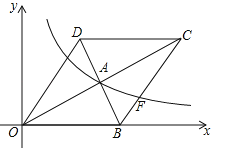
【題目】(10分)如圖,在平面直角坐標系中,菱形OBCD的邊OB在x軸上,反比例函數![]() (x>0)的圖象經過菱形對角線的交點A,且與邊BC交于點F,點A的坐標為(4,2).
(x>0)的圖象經過菱形對角線的交點A,且與邊BC交于點F,點A的坐標為(4,2).
(1)求反比例函數的表達式;
(2)求點F的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com