
【題目】如圖,在Rt△ABC中,∠B=90°,sin∠BAC= ![]() ,點D是AC上一點,且BC=BD=2,將Rt△ABC繞點C旋轉到Rt△FEC的位置,并使點E在射線BD上,連接AF交射線BD于點G,則AG的長為 .
,點D是AC上一點,且BC=BD=2,將Rt△ABC繞點C旋轉到Rt△FEC的位置,并使點E在射線BD上,連接AF交射線BD于點G,則AG的長為 . 
【答案】![]()
【解析】解:作BH⊥CD于H,如圖,
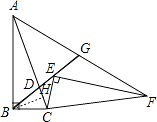
在Rt△ABC中,∠ABC=90°,∵sin∠BAC= ![]() =
= ![]() ,
,
∴AC=3BC=6,
∵BC=BD=2,
∴CH=DH,
∵∠HBC+∠ACB=90°,∠BAC+∠ACB=90°,
∴∠HBC=∠BAC,
∴sin∠HBC= ![]() ,
,
在Rt△HBC中,∵sin∠HBC= ![]() =
= ![]() ,
,
∴HC= ![]() BC=
BC= ![]() ,
,
∴CD=2CH= ![]() ,
,
∴AD=AC﹣CD=6﹣ ![]() =
= ![]() ,
,
∵Rt△ABC繞點C旋轉到Rt△FEC的位置,
∴∠BCE=∠ACF,CB=CE,CA=CF,
∴∠CBE= ![]() (180°﹣∠BCE),∠CAF=
(180°﹣∠BCE),∠CAF= ![]() (180°﹣∠ACF),
(180°﹣∠ACF),
∴∠CBE=∠CAF,
∵∠BDC=∠ADG,
∴∠AGD=∠BCD,
∵BC=BD,
∴∠BCD=∠BDC,
∴∠ADG=∠AGD,
∴AG=AD= ![]() .
.
所以答案是 ![]() .
.
【考點精析】解答此題的關鍵在于理解余角和補角的特征的相關知識,掌握互余、互補是指兩個角的數量關系,與兩個角的位置無關,以及對等腰三角形的性質的理解,了解等腰三角形的兩個底角相等(簡稱:等邊對等角).


科目:初中數學 來源: 題型:
【題目】如圖,△ABC繞著點O按順時針方向旋轉90°后到達△CDE的位置,下列說法中不正確的是( )

A. AB⊥CD
B. AC⊥CE
C. BC⊥DE
D. 點C與點B是兩個三角形的對應點
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分線分別交AB和AC于點D,E.

(1)求證:AE=2CE;
(2)連接CD,請判斷△BCD的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的文字,解答問題:
材料一:大家知道![]() 是無理數,而無理數是無限不循環小數,因此
是無理數,而無理數是無限不循環小數,因此![]() 的小數部分我們不可能全部地寫出來,于是小明用
的小數部分我們不可能全部地寫出來,于是小明用![]() 來表示
來表示![]() 的小數部分,你同意小明的表示方法嗎?事實上,小明的表示方法是有道理的,因為
的小數部分,你同意小明的表示方法嗎?事實上,小明的表示方法是有道理的,因為![]() 的整數部分是1,將這個數減去其整數部分,差就是小數部分.由此我們得到一個真命題:
的整數部分是1,將這個數減去其整數部分,差就是小數部分.由此我們得到一個真命題:
如果![]() ,其中
,其中![]() 是整數,且
是整數,且![]() 那么
那么![]() .
.
材料二:已知![]() 是有理數,并且滿足等式
是有理數,并且滿足等式![]() 求
求![]() 的值.
的值.
解:![]()
![]()
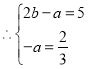 ,解得
,解得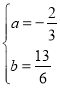
請解答:
(1)如果![]() ,其中
,其中![]() 是整數,且
是整數,且![]() 那么
那么![]() _______,
_______,![]() ______.
______.
(2)如果![]() 的小數部分為
的小數部分為![]() ,
,![]() 的整數部分為
的整數部分為![]() ,求
,求![]() 的值;
的值;
(3)已知![]() 是有理數,并且滿足等式
是有理數,并且滿足等式![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b與反比例函數y= ![]() (x>0)的圖象交于A(m,6),B(n,3)兩點.
(x>0)的圖象交于A(m,6),B(n,3)兩點. 
(1)求一次函數的解析式;
(2)根據圖象直接寫出kx+6﹣ ![]() >0時,x的取值范圍;
>0時,x的取值范圍;
(3)若M是x軸上一點,S△MOB=S△AOB , 求點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】常德市為了鼓勵市民節約用水,計劃實行生活用水按階梯式水價計費,每月用水量不超過10噸(含10噸)時,每噸按基礎價收費;每月用水量超過10噸時,超過的部分每噸按調節價收費.若王大爺家一月份用水16噸,需交水費49元,二月份用水20噸,需交水費63元.
(1)求每噸水的基礎價和調節價;
(2)若王大爺家三月份交了77元的水費,請問他家用了多少噸水?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com