
【題目】探究規律,完成相關題目.
老師說:“我定義了一種新的運算,叫(加乘)運算.”
然后老師寫出了一些按照(加乘)運算的運算法則進行運算的算式:
(+5)(+2)=+7;(-3)(-5)=+8;
(-3)(+4)=-7; (+5)(-6)=-11;
0(+8)=8;(-6)0=6.
小明看了這些算式后說:“我知道老師定義的(加乘)運算的運算法則了.”
聰明的你也明白了嗎?
(1)歸納(加乘)運算的運算法則:
兩數進行(加乘)運算時,運算法則是什么.
特別地,0和任何數進行(加乘)運算,或任何數和0進行(加乘)運算運算法則是什么.
(2)計算:
①(![]() )[
)[![]() (
(![]() )].(括號的作用與它在有理數運算中的作用一致)
)].(括號的作用與它在有理數運算中的作用一致)
② 若(![]() )(
)(![]()
![]() )
)![]() .求
.求![]() 的值.
的值.
 快捷英語周周練系列答案
快捷英語周周練系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知直線l1:y=mx(m≠0) 與直線l2:y=ax+b(a≠0) 相交于點 A(1,2),直線l2與 x軸交于點B(3,0).
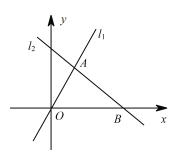
(1)分別求直線l1 和l2的表達式;
(2)過動點P(0,n)且平行于x軸的直線與l1 ,l2的交點分別為C ,D,當點 C 位于點 D 左方時,寫出 n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx﹣3經過(﹣1,0),(3,0)兩點,與y軸交于點C,直線y=kx與拋物線交于A,B兩點.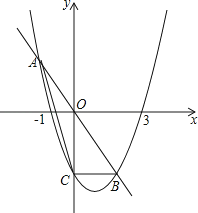
(1)寫出點C的坐標并求出此拋物線的解析式;
(2)當原點O為線段AB的中點時,求k的值及A,B兩點的坐標;
(3)是否存在實數k使得△ABC的面積為 ![]() ?若存在,求出k的值;若不存在,請說明理由.
?若存在,求出k的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
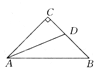
【題目】如圖所示,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,能否在AB上確定一點E,使△BDE的周長等于AB的長?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在Rt△ABC與Rt△OCD中,∠ACB=∠DCO=90°,O為AB的中點.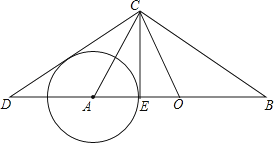
(1)求證:∠B=∠ACD.
(2)已知點E在AB上,且BC2=ABBE.
(i)若tan∠ACD= ![]() ,BC=10,求CE的長;
,BC=10,求CE的長;
(ii)試判定CD與以A為圓心、AE為半徑的⊙A的位置關系,并請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,下列結論:①b<0;②c>0;③a+c<b;④b2﹣4ac>0,其中正確的個數是( ) 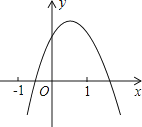
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB與坐標軸分別交于A(﹣2,0),B(0,1)兩點,與反比例函數的圖象在第一象限交于點C(4,n),求一次函數和反比例函數的解析式.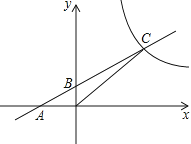
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將含有30°角的直角三角板OAB如圖放置在平面直角坐標系中,OB在x軸上,若OA=2,將三角板繞原點O順時針旋轉75°,則點A的對應點A′的坐標為( ) 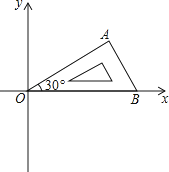
A.( ![]() ,﹣1)
,﹣1)
B.(1,﹣ ![]() )
)
C.( ![]() ,﹣
,﹣ ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
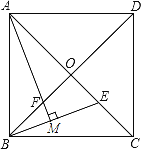
【題目】如圖,正方形ABCD的邊長為2![]() ,對角線AC、BD相交于點O,E是OC的中點,連接BE,過點A作AM⊥BE于點M,交BD于點F.
,對角線AC、BD相交于點O,E是OC的中點,連接BE,過點A作AM⊥BE于點M,交BD于點F.
(1)求證:AF=BE;
(2)求點E到BC邊的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com