
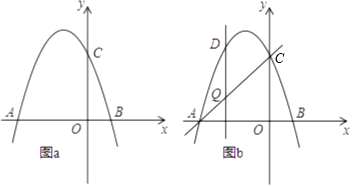
【題目】如圖,拋物線y=﹣x2+bx+c交x軸于點A(﹣3,0)和點B,交y軸于點C(0,3).
(1)求拋物線的函數表達式;
(2)若點P在拋物線上,且S△AOP=4SBOC , 求點P的坐標;
(3)如圖b,設點Q是線段AC上的一動點,作DQ⊥x軸,交拋物線于點D,求線段DQ長度的最大值
【答案】
(1)
解:把A(﹣3,0),C(0,3)代入y=﹣x2+bx+c,得
![]() ,
,
解得 ![]() .
.
故該拋物線的解析式為:y=﹣x2﹣2x+3.
(2)
解:由(1)知,該拋物線的解析式為y=﹣x2﹣2x+3,則易得B(1,0).
∵S△AOP=4S△BOC,
∴ ![]() ×3×|﹣x2﹣2x+3|=4×
×3×|﹣x2﹣2x+3|=4× ![]() ×1×3.
×1×3.
整理,得(x+1)2=0或x2+2x﹣7=0,
解得x=﹣1或x=﹣1±2 ![]() .
.
則符合條件的點P的坐標為:(﹣1,4)或(﹣1+2 ![]() ,﹣4)或(﹣1﹣2
,﹣4)或(﹣1﹣2 ![]() ,﹣4)
,﹣4)
(3)
解:設直線AC的解析式為y=kx+t,將A(﹣3,0),C(0,3)代入,
得 ![]() ,
,
解得 ![]() .
.
即直線AC的解析式為y=x+3.
設Q點坐標為(x,x+3),(﹣3≤x≤0),則D點坐標為(x,﹣x2﹣2x+3),
QD=(﹣x2﹣2x+3)﹣(x+3)=﹣x2﹣3x=﹣(x+ ![]() )2+
)2+ ![]() ,
,
∴當x=﹣ ![]() 時,QD有最大值
時,QD有最大值 ![]()
【解析】(1)把點A、C的坐標分別代入函數解析式,列出關于系數的方程組,通過解方程組求得系數的值;(2)設P點坐標為(x,﹣x2﹣2x+3),根據S△AOP=4S△BOC列出關于x的方程,解方程求出x的值,進而得到點P的坐標;(3)先運用待定系數法求出直線AC的解析式為y=x+3,再設Q點坐標為(x,x+3),則D點坐標為(x,x2+2x﹣3),然后用含x的代數式表示QD,根據二次函數的性質即可求出線段QD長度的最大值.
【考點精析】關于本題考查的二次函數的圖象和二次函數的性質,需要了解二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點;增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小才能得出正確答案.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,觀測點A、旗桿DE的底端D、某樓房CB的底端C三點在一條直線上,從點A處測得樓頂端B的仰角為22°,此時點E恰好在AB上,從點D處測得樓頂端B的仰角為38.5°.已知旗桿DE的高度為12米,試求樓房CB的高度.(參考數據:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80)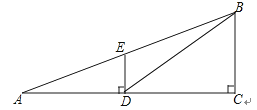
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形ABCD內接于⊙O,如圖所示,在劣弧 ![]() 上取一點E,連接DE、BE,過點D作DF∥BE交⊙O于點F,連接BF、AF,且AF與DE相交于點G,求證:
上取一點E,連接DE、BE,過點D作DF∥BE交⊙O于點F,連接BF、AF,且AF與DE相交于點G,求證: 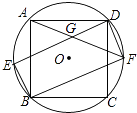
(1)四邊形EBFD是矩形;
(2)DG=BE.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,對稱軸是直線x=﹣1,下列結論:
①abc<0;②2a+b=0;③a﹣b+c>0;④4a﹣2b+c<0
其中正確的是( )
A.①②
B.只有①
C.③④
D.①④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在基地參加社會實踐話動中,帶隊老師考問學生:基地計劃新建一個矩形的生物園地,一邊靠舊墻(墻足夠長),另外三邊用總長69米的不銹鋼柵欄圍成,與墻平行的一邊留一個寬為3米的出入口,如圖所示,如何設計才能使園地的面積最大?下面是兩位學生爭議的情境: 
請根據上面的信息,解決問題:
(1)設AB=x米(x>0),試用含x的代數式表示BC的長;
(2)請你判斷誰的說法正確,為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在基地參加社會實踐話動中,帶隊老師考問學生:基地計劃新建一個矩形的生物園地,一邊靠舊墻(墻足夠長),另外三邊用總長69米的不銹鋼柵欄圍成,與墻平行的一邊留一個寬為3米的出入口,如圖所示,如何設計才能使園地的面積最大?下面是兩位學生爭議的情境: 
請根據上面的信息,解決問題:
(1)設AB=x米(x>0),試用含x的代數式表示BC的長;
(2)請你判斷誰的說法正確,為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正七邊形ABCDEFG,請僅用無刻度的直尺,分別按下列要求畫圖. 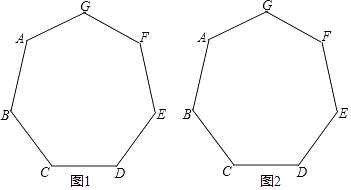
(1)在圖1中,畫出一個以AB為邊的平行四邊形;
(2)在圖2中,畫出一個以AF為邊的菱形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com