
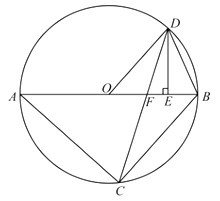
【題目】如圖,已知 ![]() 內接于
內接于 ![]() ,
, ![]() 是直徑,點
是直徑,點 ![]() 在
在 ![]() 上,
上, ![]() ,過點
,過點 ![]() 作
作 ![]() ,垂足為
,垂足為 ![]() ,連接
,連接 ![]() 交
交 ![]() 邊于點
邊于點 ![]() .
.
(1)求證: ![]() ∽
∽ ![]() ;
;
(2)求證: ![]() ;
;
(3)連接 ![]() ,設
,設 ![]() 的面積為
的面積為 ![]() ,四邊形
,四邊形 ![]() 的面積為
的面積為 ![]() ,若
,若 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)
證明:∵AB是圓O的直徑,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD//BC,
∴∠DOE=∠ABC,
∴△DOE~△ABC,
(2)
證明:∵△DOE~△ABC,
∴∠ODE=∠A,
∵∠A和∠BDC是弧BC所對的圓周角,
∴∠A=∠BDC,
∴∠ODE=∠BDC,
∴∠ODF=∠BDE。
(3)
解:因為△DOE~△ABC ,
所以![]() ,
,
即![]() =4
=4![]() =4
=4![]()
因為OA=OB,
所以![]() =
=![]() ,即
,即![]() =2
=2![]() ,
,
因為![]() =
=![]() ,S2=
,S2=![]() +
+![]() +
+![]() =2S1+S1+
=2S1+S1+![]() ,
,
所以![]() =
=![]() ,
,
所以BE=![]() OE,即OE=
OE,即OE=![]() OB=
OB=![]() OD,
OD,
所以sinA=sin∠ODE=![]() =
=![]()
【解析】(1)易證∠DEO=∠ACB=90°和∠DOE=∠ABC,根據“有兩對角相等的兩個三角形相似”判定△DOE~△ABC;
(2)由△DOE~△ABC,可得∠ODE=∠A,由∠A和∠BDC是弧BC所對的圓周角,則∠A=∠BDC,從而通過角的等量代換即可證得;
(3)由∠ODE=∠A,可得sinA=sin∠ODE=![]() =
=![]() ;而由△DOE~△ABC ,可得
;而由△DOE~△ABC ,可得![]() , 即
, 即![]() =4
=4![]() =4
=4![]()
![]() =
=![]() , 即
, 即![]() =2
=2![]() ,又因為
,又因為![]() =
=![]() ,S2=
,S2=![]() +
+![]() +
+![]() =2S1+S1+
=2S1+S1+![]() ,則可得
,則可得![]() =
=![]() , 可求得OE與OB的比值.
, 可求得OE與OB的比值.
【考點精析】認真審題,首先需要了解圓周角定理(頂點在圓心上的角叫做圓心角;頂點在圓周上,且它的兩邊分別與圓有另一個交點的角叫做圓周角;一條弧所對的圓周角等于它所對的圓心角的一半),還要掌握相似三角形的性質(對應角相等,對應邊成比例的兩個三角形叫做相似三角形)的相關知識才是答題的關鍵.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數學 來源: 題型:
【題目】觀察下列等式:
① ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
② ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
③ ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
④ ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() ;
;
…
(1)請按以上規律寫出第⑤個等式:;
(2)猜想并寫出第n個等式:;
(3)請證明猜想的正確性.
查看答案和解析>>
科目:初中數學 來源: 題型:
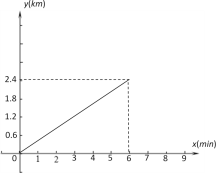
【題目】已知A、B兩地相距2.4km,甲騎車勻速從A地前往B地,如圖表示甲騎車過程中離A地的路程y(km)與他行駛所用的時間x(min)之間的關系.根據圖像解答下列問題:
(1)甲騎車的速度是 km/min;
(2)若在甲出發時,乙在甲前方0.6km處,兩人均沿同一路線同時出發勻速前往B地,在第3分鐘甲追上了乙,兩人到達B地后停止.請在下面同一平面直角坐標系中畫出乙離A地的距離y乙(km)與所用時間x(min)的關系的大致圖像;
(3)乙在第幾分鐘到達B地?
(4)兩人在整個行駛過程中,何時相距0.2km?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A是雙曲線y= ![]() (x>0)上的一動點,過A作AC⊥y軸,垂足為點C,作AC的垂直平分線交雙曲線于點B,交x軸于點D.當點A在雙曲線上從左到右運動時,對四邊形ABCD的面積的變化情況,小明列舉了四種可能:
(x>0)上的一動點,過A作AC⊥y軸,垂足為點C,作AC的垂直平分線交雙曲線于點B,交x軸于點D.當點A在雙曲線上從左到右運動時,對四邊形ABCD的面積的變化情況,小明列舉了四種可能:
①逐漸變小;
②由大變小再由小變大;
③由小變大再由大變小;
④不變.
你認為正確的是 . (填序號)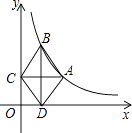
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD內接于⊙O,AB是⊙O的直徑,點P在CA的延長線上,∠CAD=45°.
(Ⅰ)若AB=4,求 ![]() 的長;
的長;
(Ⅱ)若 ![]() =
= ![]() ,AD=AP,求證:PD是⊙O的切線.
,AD=AP,求證:PD是⊙O的切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種產品的年產量不超過1 000t,該產品的年產量(t)與費用(萬元)之間的函數關系如圖(1);該產品的年銷售量(t)與每噸銷售價(萬元)之間的函數關系如圖(2).若生產出的產品都能在當年銷售完,則年產量為多少噸時,當年可獲得7500萬元毛利潤?(毛利潤=銷售額﹣費用)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一輪船由![]() 處向
處向![]() 處航行,在
處航行,在![]() 處測得
處測得![]() 處在
處在![]() 的北偏東
的北偏東![]() 方向上,在海島上的觀察所
方向上,在海島上的觀察所![]() 測得
測得![]() 在
在![]() 的南偏西
的南偏西![]() 方向上,
方向上,![]() 在
在![]() 的南偏東
的南偏東![]() 方向.若輪船行駛到
方向.若輪船行駛到![]() 處,那么從
處,那么從![]() 處看
處看![]() ,
,![]() 兩處的視角
兩處的視角![]() 是多少度?
是多少度?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在△ABC和△DBC中,∠ACB=∠DBC=90°,點E是BC的中點,EF⊥AB,垂足為F,且AB=DE.

(1)求證:△BCD是等腰直角三角形;
(2)若BD=8厘米,求AC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com