
【題目】如圖,AB=16,O為AB中點,點C在線段OB上(不與點O,B重合),將OC繞點O逆時針旋轉270°后得到扇形COD,AP,BQ分別切優弧 ![]() 于點P,Q,且點P,Q在AB異側,連接OP.
于點P,Q,且點P,Q在AB異側,連接OP. 
(1)求證:AP=BQ;
(2)當BQ=4 ![]() 時,求
時,求 ![]() 的長(結果保留π);
的長(結果保留π);
(3)若△APO的外心在扇形COD的內部,求OC的取值范圍.
【答案】
(1)證明:連接OQ.

∵AP、BQ是⊙O的切線,
∴OP⊥AP,OQ⊥BQ,
∴∠APO=∠BQO=90°,
在Rt△APO和Rt△BQO中,
![]() ,
,
∴Rt△APO≌Rt△BQO,
∴AP=BQ
(2)解:∵Rt△APO≌Rt△BQO,
∴∠AOP=∠BOQ,
∴P、O、Q三點共線,
∵在Rt△BOQ中,cosB= ![]() =
= ![]() =
= ![]() ,
,
∴∠B=30°,∠BOQ=60°,
∴OQ= ![]() OB=4,
OB=4,
∵∠COD=90°,
∴∠QOD=90°+60°=150°,
∴優弧 ![]() 的長=
的長= ![]() =
= ![]() π
π
(3)解:∵△APO的外心是OA的中點,OA=8,
∴△APO的外心在扇形COD的內部時,OC的取值范圍為4<OC<8
【解析】(1)連接OQ.只要證明Rt△APO≌Rt△BQO即可解決問題;(2)求出優弧DQ的圓心角以及半徑即可解決問題;(3)由△APO的外心是OA的中點,OA=8,推出△APO的外心在扇形COD的內部時,OC的取值范圍為4<OC<8;
【考點精析】解答此題的關鍵在于理解切線的性質定理的相關知識,掌握切線的性質:1、經過切點垂直于這條半徑的直線是圓的切線2、經過切點垂直于切線的直線必經過圓心3、圓的切線垂直于經過切點的半徑,以及對弧長計算公式的理解,了解若設⊙O半徑為R,n°的圓心角所對的弧長為l,則l=nπr/180;注意:在應用弧長公式進行計算時,要注意公式中n的意義.n表示1°圓心角的倍數,它是不帶單位的.


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC中,∠C=90°,∠BAC的平分線AD交BC于點D,過點D作DE⊥AD交AB于點E,以AE為直徑作⊙O. 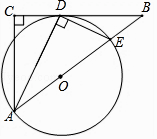
(1)求證:BC是⊙O的切線;
(2)若AC=3,BC=4,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,![]() 和
和![]() 都是邊長為1的等邊三角形.
都是邊長為1的等邊三角形.
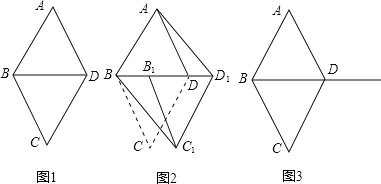
![]() 四邊形ABCD是菱形嗎?為什么?
四邊形ABCD是菱形嗎?為什么?
![]() 如圖2,將
如圖2,將![]() 沿射線BD方向平移到
沿射線BD方向平移到![]() 的位置,則四邊形
的位置,則四邊形![]() 是平行四邊形嗎?為什么?
是平行四邊形嗎?為什么?
![]() 在
在![]() 移動過程中,四邊形
移動過程中,四邊形![]() 有可能是矩形嗎?如果是,請求出點B移動的距離
有可能是矩形嗎?如果是,請求出點B移動的距離![]() 寫出過程
寫出過程![]() ;如果不是,請說明理由
;如果不是,請說明理由![]() 圖3供操作時使用
圖3供操作時使用![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
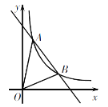
【題目】如圖,在直角坐標系xOy中,一次函數y=k1x+b的圖象與反比例函數y=![]() 的圖象交于A(1,4),B(3,m)兩點.
的圖象交于A(1,4),B(3,m)兩點.
(1)求反比例函數和一次函數的解析式;
(2)求△AOB的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com