
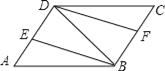
【題目】如圖,在ABCD中,連接對角線BD,BE平分∠ABD交AD于點E,DF平分∠BDC交BC于點F.
(1)求證:△AEB≌△CFD;
(2)若BD=BA,試判斷四邊形DEBF的形狀,并加以證明.
【答案】(1)證明見解析;(2)四邊形DEBF是矩形;理由見解析.
【解析】分析:(1)由平行四邊形的性質得出AD∥BC,CD∥BA,∠A=∠C,AB=CD,得出∠ABD=∠BDC,由角平分線的定義證出∠DBE=∠FDB,由ASA證明△AEB≌△CFD即可;(2)先證明四邊形DEBF是平行四邊形,再根據等腰三角形的“三線合一”的性質推知BE⊥AD,然后由“有一內角為直角的平行四邊形是矩形”證得四邊形DEBF是矩形即可.
本題解析:(1)證明:∵四邊形ABCD是平行四邊形,
∴AD∥BC,CD∥BA,∠A=∠C,AB=CD,
∴∠ABD=∠BDC(兩直線平行,內錯角相等).
又∵BE平分∠ABD,DF平分∠BDC,
∴∠ABE=∠DBE=![]() ∠ABD,∠CDF=∠BDF=
∠ABD,∠CDF=∠BDF=![]() ∠BDC,
∠BDC,
∴∠DBE=∠FDB=∠DBE=∠BDF(等量代換),
在△AEB和△CFD中, 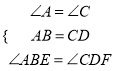 ,
,
∴△AEB≌△CFD(ASA);
(2)解:四邊形DEBF是矩形;理由如下:
由(1)知:∠DBE=∠BDF,
∴BE∥DF,
∵DE∥BF,
∴四邊形EBFD是平行四邊形.
∵BD=BA,BE是∠ABD的平分線,
∴BE⊥AD,
∴∠DEB=90°,
∴四邊形DEBF是矩形(有一內角為直角的平行四邊形是矩形).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖 1,二次函數![]() 的圖像過點 A (3,0),B (0,4)兩點,動點 P 從 A 出發,在線段 AB 上沿 A → B 的方向以每秒 2 個單位長度的速度運動,過點P作 PD⊥y 于點 D ,交拋物線于點 C .設運動時間為 t (秒).
的圖像過點 A (3,0),B (0,4)兩點,動點 P 從 A 出發,在線段 AB 上沿 A → B 的方向以每秒 2 個單位長度的速度運動,過點P作 PD⊥y 于點 D ,交拋物線于點 C .設運動時間為 t (秒).
(1)求二次函數![]() 的表達式;
的表達式;
(2)連接 BC ,當t=![]() 時,求△BCP的面積;
時,求△BCP的面積;
(3)如圖 2,動點 P 從 A 出發時,動點 Q 同時從 O 出發,在線段 OA 上沿 O→A 的方向以 1個單位長度的速度運動,當點 P 與 B 重合時,P 、 Q 兩點同時停止運動,連接 DQ 、 PQ ,將△DPQ沿直線 PC 折疊到 △DPE .在運動過程中,設 △DPE 和 △OAB重合部分的面積為 S ,直接寫出 S 與 t 的函數關系式及 t 的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
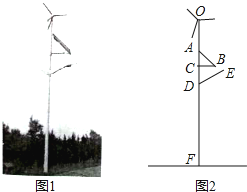
【題目】如圖1,濱海廣場裝有風能、太陽能發電的風光互補環保路燈,燈桿頂端裝有風力發電機,中間裝有太陽能板,下端裝有路燈.該系統工作過程中某一時刻的截面圖如圖2,已知太陽能板的支架BC垂直于燈桿OF,路燈頂端E距離地面6米,DE=1.8米,∠CDE=60°.且根據我市的地理位置設定太陽能板AB的傾斜角為43°.AB=1.5米,CD=1米,為保證長為1米的風力發電機葉片無障礙安全旋轉,對葉片與太陽能板頂端A的最近距離不得少于0.5米,求燈桿OF至少要多高?(利用科學計算器可求得sin43°≈0.6820,cos43°≈0.7314,tan43°≈0.9325,結果保留兩位小數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:●和○兩種圓按某種規則排列,則前2017個圓中有○ 個.( )
○●○●●○●●●○●○●●○●●●○●○●●○●●●……
A. 671 B. 672 C. 673 D. 674
查看答案和解析>>
科目:初中數學 來源: 題型:
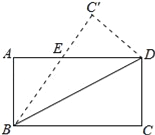
【題目】如圖,在矩形ABCD中,BC=6cm,CD=3cm,將△BCD沿BD翻折,點C落在點C′處,BC′交AD于點E,則AE的長為______ cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列因式分解中,是利用提公因式法分解的是( )
A. a2﹣b2=(a+b)(a﹣b) B. a2﹣2ab+b2=(a﹣b)2
C. ab+ac=a(b+c) D. a2+2ab+b2=(a+b)2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com