
【題目】在初中數學學習階段,我們常常會利用一些變形技巧來簡化式子,解答問題.
材料一:在解決某些分式問題時,倒數法是常用的變形技巧之一,所謂倒數法,即把式子變成其倒數形式,從而運用約分化簡,以達到計算目的.
例:已知:![]() ,求代數式x2+
,求代數式x2+![]() 的值.
的值.
解:∵![]() ,∴
,∴![]() =4
=4
即![]() =4∴x+
=4∴x+![]() =4∴x2+
=4∴x2+![]() =(x+
=(x+![]() )2﹣2=16﹣2=14
)2﹣2=16﹣2=14
材料二:在解決某些連等式問題時,通常可以引入參數“k”,將連等式變成幾個值為k的等式,這樣就可以通過適當變形解決問題.
例:若2x=3y=4z,且xyz≠0,求![]() 的值.
的值.
解:令2x=3y=4z=k(k≠0)
則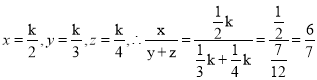
根據材料回答問題:
(1)已知![]() ,求x+
,求x+![]() 的值.
的值.
(2)已知![]() ,(abc≠0),求
,(abc≠0),求![]() 的值.
的值.
(3)若![]() ,x≠0,y≠0,z≠0,且abc=7,求xyz的值.
,x≠0,y≠0,z≠0,且abc=7,求xyz的值.
【答案】(1)5;
(2)![]() ;
;
(3)![]()
【解析】
(1)仿照材料一,取倒數,再約分,利用等式的性質求解即可;
(2)仿照材料二,設![]() =
=![]() =
=![]() =k(k≠0),則a=5k,b=2k,c=3k,代入所求式子即可;
=k(k≠0),則a=5k,b=2k,c=3k,代入所求式子即可;
(3)本題介紹兩種解法:
解法一:(3)解法一:設![]() =
=![]() =
=![]() =
=![]() (k≠0),化簡得:
(k≠0),化簡得:![]() ①,
①,![]() ②,
②,![]() ③,相加變形可得x、y、z的代入
③,相加變形可得x、y、z的代入![]() =
=![]() 中,可得k的值,從而得結論;
中,可得k的值,從而得結論;
解法二:取倒數得:![]() =
=![]() =
=![]() ,拆項得
,拆項得![]() ,從而得x=
,從而得x=![]() ,z=
,z=![]() ,代入已知可得結論.
,代入已知可得結論.
解:(1)∵![]() =
=![]() ,
,
∴![]() =4,
=4,
∴x﹣1+![]() =4,
=4,
∴x+![]() =5;
=5;
(2)∵設![]() =
=![]() =
=![]() =k(k≠0),則a=5k,b=2k,c=3k,
=k(k≠0),則a=5k,b=2k,c=3k,
∴![]() =
=![]() =
=![]() =
=![]() ;
;
(3)解法一:設![]() =
=![]() =
=![]() =
=![]() (k≠0),
(k≠0),
∴![]() ①,
①,![]() ②,
②,![]() ③,
③,
①+②+③得:2(![]() )=3k,
)=3k,
![]() =
=![]() k④,
k④,
④﹣①得:![]() =
=![]() k,
k,
④﹣②得:![]() ,
,
④﹣③得:![]() k,
k,
∴x=![]() ,y=
,y=![]() ,z=
,z=![]() 代入
代入![]() =
=![]() 中,得:
中,得:
 =
=![]() ,
,
![]() ,
,
k=4,
∴x=![]() ,y=
,y=![]() ,z=
,z=![]() ,
,
∴xyz=![]() =
=![]() =
=![]() ;
;
解法二:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
將其代入![]() 中得:
中得:  =
=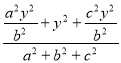
![]() =
=![]() ,y=
,y=![]() ,
,
∴x=![]() ,z=
,z=![]() =
=![]() ,
,
∴xyz=![]() =
=![]() .
.


 一線名師提優試卷系列答案
一線名師提優試卷系列答案 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源: 題型:
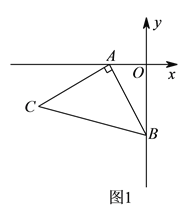
【題目】如圖![]() ,
, ![]() ,
, ![]() ,以
,以![]() 點為頂點、
點為頂點、![]() 為腰在第三象限作等腰
為腰在第三象限作等腰![]() .
.
(![]() )求
)求![]() 點的坐標.
點的坐標.
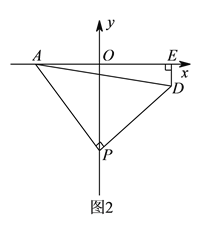
(![]() )如圖
)如圖![]() ,
, ![]() 為
為![]() 軸負半軸上一個動點,當
軸負半軸上一個動點,當![]() 點沿
點沿![]() 軸負半軸向下運動時,以
軸負半軸向下運動時,以![]() 為頂點,
為頂點, ![]() 為腰作等腰
為腰作等腰![]() ,過
,過![]() 作
作![]() 軸于
軸于![]() 點,求
點,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】等腰Rt△ABC中,∠BAC=90°,AB=AC,點A、點B分別是y軸、x軸上兩個動點,直角邊AC交x軸于點D,斜邊BC交y軸于點E;

(1)如圖(1),已知C點的橫坐標為-1,直接寫出點A的坐標;
(2)如圖(2), 當等腰Rt△ABC運動到使點D恰為AC中點時,連接DE,求證:∠ADB=∠CDE;
(3)如圖(3), 若點A在x軸上,且A(-4,0),點B在y軸的正半軸上運動時,分別以OB、AB為直角邊在第一、二象限作等腰直角△BOD和等腰直角△ABC,連結CD交y軸于點P,問當點B在y軸的正半軸上運動時,BP的長度是否變化?若變化請說明理由,若不變化,請求出BP的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD的對角線AC、BD相交于點O,AB⊥AC,AB=3,BC=5,點P從點A出發,沿AD以每秒1個單位的速度向終點D運動.連結PO并延長交BC于點Q.設點P的運動時間為t秒.
(1)求BQ的長,(用含t的代數式表示)
(2)當四邊形ABQP是平行四邊形時,求t的值
(3)當點O在線段AP的垂直平分線上時,直接寫出t的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】( 1)計算:![]() ﹣4sin30°+(2015﹣π)0﹣(﹣3)2
﹣4sin30°+(2015﹣π)0﹣(﹣3)2
(2)先化簡,再求值:1﹣![]() ,其中x、y滿足|x﹣2|+(2x﹣y﹣3)2=0.
,其中x、y滿足|x﹣2|+(2x﹣y﹣3)2=0.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P為定角∠AOB的平分線上的一個定點,且∠MPN與∠AOB互補,若∠MPN在繞點P旋轉的過程中,其兩邊分別與OA、OB相交于M、N兩點,則以下結論:(1)PM=PN恒成立;(2)OM+ON的值不變;(3)四邊形PMON的面積不變;(4)MN的長不變,其中正確的個數為( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖中實線所示,函數y=|a(x﹣1)2﹣1|的圖象經過原點,小明同學研究得出下面結論:
①a=1;②若函數y隨x的增大而減小,則x的取值范圍一定是x<0;
③若方程|a(x﹣1)2﹣1|=k有兩個實數解,則k的取值范圍是k>1;
④若M(m1,n),N(m2,n),P(m3,n),Q(m4,n)(n>0)是上述函數圖象的四個不同點,且m1<m2<m3<m4,則有m2+m3﹣m1=m4.其中正確的結論有( )

A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 在
在![]() 軸上,
軸上,![]() ,
,![]() ,
,![]() ,將
,將![]() 繞點
繞點![]() 按順時針方向旋轉
按順時針方向旋轉![]() 得到
得到![]() ,則點
,則點![]() 的坐標是( )
的坐標是( )

A. (2,-2![]() ) B. (2,-2
) B. (2,-2![]() ) C. (2
) C. (2![]() ,2) D. (2
,2) D. (2![]() ,2)
,2)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com