
【題目】在不透明的袋子中有四張標著數字1,2,3,4的卡片,小明、小華兩人按照各自的規則玩抽卡片游戲.
小明畫出樹狀圖如圖所示:
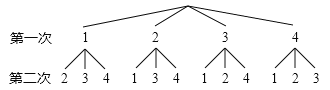
小華列出表格如下:

回答下列問題:
(1)根據小明畫出的樹形圖分析,他的游戲規則是,隨機抽出一張卡片后 (填“放回”或“不放回”),再隨機抽出一張卡片;
(2)根據小華的游戲規則,表格中①表示的有序數對為 ;
(3)規定兩次抽到的數字之和為奇數的獲勝,你認為誰獲勝的可能性大?為什么?
【答案】(1)不放回;(2)(3,2);(3)小明獲勝的可能性大.
【解析】試題分析:(1)根據小明畫出的樹形圖知數字1在第一次中出現,但沒有在第二次中出現可以判斷;
(2)根據橫坐標表示第一次,縱坐標表示第二次可以得到答案;
(3)根據樹狀圖和統計表分別求得其獲勝的概率,比較后即可得到答案.
試題解析:解:(1)觀察樹狀圖知:第一次摸出的數字沒有在第二次中出現,∴小明的實驗是一個不放回實驗;
(2)(3,2);
(3)小明獲勝的可能性大.理由如下:
∵根據小明的游戲規則,共有12種等可能的結果,數字之和為奇數的有8種,∴概率為: ![]() =
=![]() ;∵根據小華的游戲規則,共有16種等可能的結果,數字之和為奇數的有8種,∴概率為:
;∵根據小華的游戲規則,共有16種等可能的結果,數字之和為奇數的有8種,∴概率為: ![]() =
=![]() >
>![]() ,∴小明獲勝的可能性大.
,∴小明獲勝的可能性大.
故答案為:不放回;(3,2).


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:初中數學 來源: 題型:
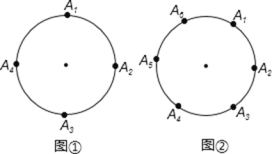
【題目】如圖①,如果 A1、A2、A3、A4 把圓周四等分,則以A1、A2、A3、A4為頂點的直角三角形4個;如圖②,如果A1、A2、A3、A4、A5、A6 把圓周六等分,則以A1、A2、A3、A4、A5、A6 為點的直角三角形有 12 個;如果 A1、A2、A3、……A2n 把圓周 2n 等分,則以 A1、A2、A3、…A2n為頂點的直角三角形有__________個,
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,用同樣規格黑白兩色的正方形瓷磚鋪設長方形地面,請觀察下列圖形,并解答有關問題:
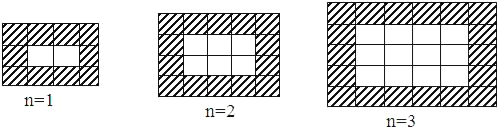
(1)在第n個圖中,第一橫行共 塊瓷磚,第一豎列共有 塊瓷磚;(均用含n的代數式表示)鋪設地面所用瓷磚的總塊數為 (用含n的代數式表示,n表示第n個圖形)
(2)上述鋪設方案,鋪一塊這樣的長方形地面共用了506塊瓷磚,求此時n的值;
(3)黑瓷磚每塊4元,白瓷磚每塊3元,在問題(2)中,共需要花多少錢購買瓷磚?
(4)是否存在黑瓷磚與白瓷磚塊數相等的情形?請通過計算加以說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,等腰直角三角形OA1A2的直角邊OA1在y軸的正半軸上,且OA1=A1A2=1,以OA2為直角邊作第二個等腰直角三角形OA2A3,以OA3為直角邊作第三個等腰直角三角形OA3A4,…,依此規律,得到等腰直角三角形OA2017A2018,則點A2017的坐標為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一副三角板中的兩塊直角三角尺的直角頂點![]() 按如圖方式疊放在一起.
按如圖方式疊放在一起.
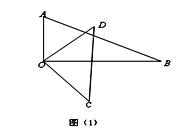
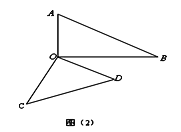
(1)如圖(1)若![]() ,求
,求![]() 的度數,若
的度數,若![]() ,求
,求![]() 的度數;
的度數;
(2)如圖(2)若![]() ,求
,求![]() 的度數;
的度數;
(3)猜想![]() 與
與![]() 的數量關系,并結合圖(1)說明理由;
的數量關系,并結合圖(1)說明理由;
(4)三角尺![]() 不動,將三角尺
不動,將三角尺![]() 的
的![]() 邊與
邊與![]() 邊重合,然后繞點
邊重合,然后繞點![]() 按順時針或逆時針方向任意轉動一個角度,當
按順時針或逆時針方向任意轉動一個角度,當![]() (
(![]() )等于多少度時,這兩塊三角尺各有一條邊互相垂直,直接寫出
)等于多少度時,這兩塊三角尺各有一條邊互相垂直,直接寫出![]() 角度所有可能的值,不用說明理由.
角度所有可能的值,不用說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從2開始,連續的偶數相加,它們和的情況如下表:
加數的個數 | 連續偶數的和 |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
(1)如果![]() 時,那么
時,那么![]() 的值為______;
的值為______;
(2)根據表中的規律猜想:用含有![]() 的代數式表示
的代數式表示![]() 的公式為:
的公式為:![]() ______;
______;
(3)根據上題的規律計算![]() 的值(要有計算過程).
的值(要有計算過程).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場統計了每個營業員在某月的銷售額,繪制了如下的條形統計圖以及不完整的扇形統計圖:
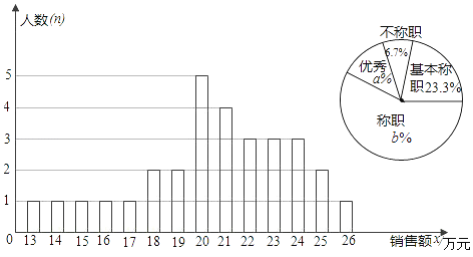
解答下列問題:
(1)設營業員的月銷售額為x(單位:萬元),商場規定:當x<15時為不稱職,當15≤x<20時,為基本稱職,當20≤x<25為稱職,當x≥25時為優秀.則扇形統計圖中的a=________,b=________.
(2)所有營業員月銷售額的中位數和眾數分別是多少?
(3)為了調動營業員的積極性,決定制定一個月銷售額獎勵標準,凡到達或超過這個標準的營業員將受到獎勵.如果要使得營業員的半數左右能獲獎,獎勵標準應定為多少萬元?并簡述其理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點P是菱形ABCD的對角線AC上的一個動點,已知AB=1,∠ADC=120°, 點M,N分別是AB,BC邊上的中點,則△MPN的周長最小值是______.
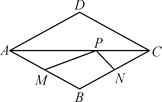
查看答案和解析>>
科目:初中數學 來源: 題型:
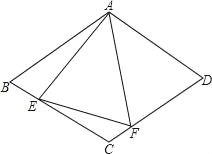
【題目】如圖,在菱形ABCD中,AB=4,∠BAD=120°,△AEF為正三角形,E、F在菱形的邊BC,CD上.
(1)證明:BE=CF.
(2)當點E,F分別在邊BC,CD上移動時(△AEF保持為正三角形),請探究四邊形AECF的面積是否發生變化?若不變,求出這個定值;如果變化,求出其最大值.
(3)在(2)的情況下,請探究△CEF的面積是否發生變化?若不變,求出這個定值;如果變化,求出其最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com