
【題目】如圖,已知函數y=x+2的圖象與y軸交于點A,一次函數y=kx+b的圖象經過點B(0,4)且與x軸及y=x+2的圖象分別交于點C、D,點D的坐標為(![]() ,n)
,n)

(1)則n= ,k= ,b=_______.
(2)若函數y=kx+b的函數值大于函數y=x+2的函數值,則x的取值范圍是_______.
(3)求四邊形AOCD的面積.
【答案】(1)![]() ,2,4;(2)x<
,2,4;(2)x<![]() ;(3)
;(3)![]() .
.
【解析】
(1)根據點D在函數y=x+2的圖象上,即可求出n的值;再利用待定系數法求出k,b的值;
(2)根據圖象,直接判斷即可;
(3)用三角形OBC的面積減去三角形ABD的面積即可.
(1)∵點D(![]() ,n)在直線y=x+2上,
,n)在直線y=x+2上,
∴n=![]() +2=
+2=![]() ,
,
∵一次函數經過點B(0,4)、點D(![]() ,
, ![]() ),
),
∴ ,解得:
,解得:![]() ,
,
故答案為:![]() ,2,4;
,2,4;
(2)由圖象可知,函數y=kx+b大于函數y=x+2時,圖象在直線x=![]() 的左側,
的左側,

∴x<![]() ,
,
故答案為:x<![]() ,
,
(3)直線y=2x+4與x軸交于點C,
∴令y=0,得:2x+4=0,解得x=2,
∴點C的坐標為(2,0),
∵函數y=x+2的圖象與y軸交于點A,
∴令x=0,得:y=2,
∴點A的坐標為(0,2),
S![]() =
=![]() ×2×4=4,
×2×4=4,
S![]() =
=![]() ×(42)×
×(42)×![]() =
=![]() ,
,
∴S![]() =S
=S![]() =4
=4![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() 、
、![]() ,與雙曲線
,與雙曲線![]() 交于第一象限的點
交于第一象限的點![]() 和第三象限的點
和第三象限的點![]() ,
,![]() 點的縱坐標為
點的縱坐標為![]()
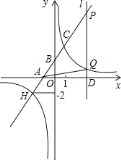
![]() 求
求![]() 和
和![]() 的值;
的值;
![]() 求不等式:
求不等式:![]() 的解集
的解集
![]() 過
過![]() 軸上的點
軸上的點![]() 作平行于
作平行于![]() 軸的直線
軸的直線![]() ,分別與直線
,分別與直線![]() 和雙曲線
和雙曲線![]() 交于點
交于點![]() 、
、![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,湛河兩岸AB與EF平行,小亮同學假期在湛河邊A點處,測得對岸河邊C處視線與湛河岸的夾角∠CAB=37°,沿河岸前行140米到點B處,測得對岸C處的視線與湛河岸夾角∠CBA=45°.問湛河的寬度約多少米?(參考數據:sin37°≈0.60,cos37°=0.80,tan37°=0.75)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點P(3m-6,m+1),試分別根據下列條件,求出點P的坐標.
(1)點P的橫坐標比縱坐標大1;
(2)點P在過點A(3,-2),且與x軸平行的直線上;
(3)點P到y軸的距離是到x軸距離的2倍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(11·西寧)西寧中心廣場有各種音樂噴泉,其中一個噴水管的最大高度為3米,此時距噴水管的水平距離為![]() 米,在如圖3所示的坐標系中,這個噴泉的函數關系式是
米,在如圖3所示的坐標系中,這個噴泉的函數關系式是
A. y=-(x-![]() )x2+3 B. y=-3(x+
)x2+3 B. y=-3(x+![]() )x2+3
)x2+3
C. y=-12(x-![]() )x2+3 D. y=-12(x+
)x2+3 D. y=-12(x+![]() )x2+3
)x2+3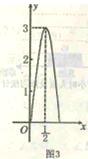
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在銳角△ABC中,AC=8,△ABC的面積為20,∠BAC的平分線交BC于點D,M,N分別是AD和AB上的動點,則BM+MN的最小值是________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC中,AB=AC,點E在△ABC外一點,CE⊥AE于點E,CE=![]() BC.
BC.
(1)作出△ABC的角平分線AD.(要求:尺規作圖,不寫作法,保留作圖痕跡.)
(2)求證:∠ACE=∠B.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某港口有一燈塔![]() ,燈塔
,燈塔![]() 的正東有
的正東有![]() 、
、![]() 兩燈塔,以
兩燈塔,以![]() 為直徑的半圓區域內有若干暗礁,
為直徑的半圓區域內有若干暗礁,![]() 海里,一船在
海里,一船在![]() 處測得燈塔
處測得燈塔![]() 、
、![]() 分別在船的
分別在船的
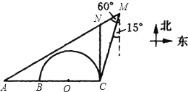
南偏西![]() 和南偏西
和南偏西![]() 方向,船沿
方向,船沿![]() 方向行駛
方向行駛![]() 海里恰好處在燈塔
海里恰好處在燈塔![]() 的正北方向
的正北方向![]() 處.
處.
![]() 求
求![]() 的長(精確到
的長(精確到![]() 海里);
海里);
![]() 若船繼續沿
若船繼續沿![]() 方向朝
方向朝![]() 行駛,是否有觸礁的危險?
行駛,是否有觸礁的危險?
(參考數值:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(新知學習)
如果一個三角形有一邊上的中線等于這條邊的一半,那么我們就把這樣的三角形叫做“智慧三角形”.
(簡單運用)
(1)下列三個三角形,是智慧三角形的是______(填序號);

(2)如圖,已知等邊三角形![]() ,請用刻度尺在該三角形邊上找出所有滿足條件的點
,請用刻度尺在該三角形邊上找出所有滿足條件的點![]() ,使
,使![]() 為“智慧三角形”,并寫出作法;
為“智慧三角形”,并寫出作法;

(深入探究)
(3)如圖,在正方形![]() 中,點
中,點![]() 是
是![]() 的中點,
的中點,![]() 是
是![]() 上一點,且
上一點,且![]() ,試判斷
,試判斷![]() 是否為“智慧三角形”,并說明理由;
是否為“智慧三角形”,并說明理由;

(靈活應用)
(4)如圖,等邊三角形![]() 邊長
邊長![]() .若動點
.若動點![]() 以
以![]() 的速度從點
的速度從點![]() 出發,沿
出發,沿![]() 的邊
的邊![]() 運動.若另一動點
運動.若另一動點![]() 以
以![]() 的速度從點
的速度從點![]() 出發,沿邊
出發,沿邊![]() 運動,兩點同時出發,當點
運動,兩點同時出發,當點![]() 首次回到點
首次回到點![]() 時,兩點同時停止運動.設運動時間為
時,兩點同時停止運動.設運動時間為![]() ,那么
,那么![]() 為______
為______![]() 時,
時,![]() 為“智慧三角形”.
為“智慧三角形”.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com