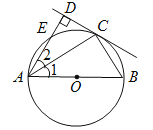
【題目】（滿分10分）如圖，AB為⊙O的直徑，點E在⊙O上，C為
的中點，過點C作直線CD⊥AE于D，連接AC，BC．
（1）試判斷直線CD與⊙O的位置關系，并說明理由；
（2）若AD=2，AC=
，求AB的長．
【答案】（1）相切；（2）3．
【解析】
試題分析：（1）連接OC，由C為
的中點，得到∠1=∠2，等量代換得到∠2=∠ACO，根據(jù)平行線的性質得到OC⊥CD，即可得到結論；
（2）連接CE，由勾股定理得到CD的長，根據(jù)切割線定理得到
=ADDE，根據(jù)勾股定理得到CE的長，由圓周角定理得到∠ACB=90°，即可得到結論．
試題解析：（1）相切，連接OC，∵C為的中點，∴∠1=∠2，∵OA=OC，∴∠1=∠ACO，∴∠2=∠ACO，∴AD∥OC，∵CD⊥AD，∴OC⊥CD，∴直線CD與⊙O相切；
（2）方法1：連接CE，∵AD=2，AC=
，∵∠ADC=90°，∴CD=
=
，∵CD是⊙O的切線，∴=ADDE，∴DE=1，∴CE=
=
，∵C為的中點，∴BC=CE=，∵AB為⊙O的直徑，∴∠ACB=90°，∴AB=
=3．
方法2：∵∠DCA=∠B，易得△ADC∽△ACB，∴
，∴AB=3．
品學雙優(yōu)卷系列答案
小學期末沖刺100分系列答案
期末復習檢測系列答案
超能學典單元期中期末專題沖刺100分系列答案科目：初中數(shù)學 來源： 題型：
【題目】在面積為12的平行四邊形ABCD中，過點A作直線BC的垂線交直線BC于點E，過點A作直線CD的垂線交直線CD于點F，若AB＝4，BC＝6，則CE＋CF的值為.
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
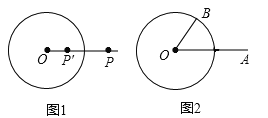
【題目】如圖1，⊙O的半徑為r（r＞0），若點P′在射線OP上，滿足OP′OP=
，則稱點P′是點P關于⊙O的“反演點”．
如圖2，⊙O的半徑為4，點B在⊙O上，∠BOA=60°，OA=8，若點A′，B′分別是點A，B關于⊙O的反演點，求A′B′的長．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】點M（﹣3，﹣5）是由N先向上平移4個單位，再向左平移3個單位而得到，則點N的坐標為（ ）
A.（0，﹣9）
B.（﹣6，﹣1）
C.（1，﹣2）
D.（1，﹣8）
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】閱讀填空：請你閱讀芳芳的說理過程并填出理由：
（1）如圖1，已知AB∥CD．
求證：∠BAE+∠DCE=∠AEC．
理由：作EF∥AB，則有EF∥CD（）
∴∠1=∠BAE，∠2=∠DCE（）
∴∠AEC=∠1+∠2=∠BAE+∠DCE（）
思維拓展：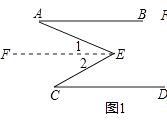
（2）如圖2，已知AB∥CD，BE平分∠ABC，DE平分∠ADC．BE、DE所在直線交于點E，若∠FAE=m°，∠ABC=n°，求∠BED的度數(shù)．（用含m、n的式子表示）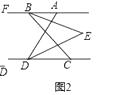
（3）將圖2中的線段BC沿DC方向平移，使得點B在點A的右側，其他條件不變，得到圖3，直接寫出∠BED的度數(shù)是（用含m、n的式子表示）．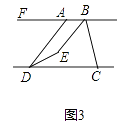
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】閱讀下面文字：
對于（﹣5 
）+（﹣9 
）+17 
+（﹣3 
）
可以如下計算：
原式=[（﹣5）+（﹣ ）]+[（﹣9）+（﹣ ）]+（17+ ）+[（﹣3）+（﹣ ）]
=[（一5）+（﹣9）+17+（一3）]+[（﹣ ）+（﹣ ）+ +（﹣ ）]
=0+（﹣1 
）
=﹣1
上面這種方法叫拆項法，你看懂了嗎？
仿照上面的方法，請你計算：（﹣2000 ）+（﹣1999 ）+4000 +（﹣1 ）．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】請閱讀下列材料，并完成相應的任務：
阿基米德折弦定理
阿基米德（archimedes，公元前287﹣公元前212年，古希臘）是有史以來最偉大的數(shù)學家之一，他與牛頓、高斯并成為三大數(shù)學王子．
阿拉伯Al﹣Binmi（973﹣1050年）的譯文中保存了阿基米德折弦定理的內(nèi)容，蘇聯(lián)在1964年根據(jù)Al﹣Binmi譯本出版了俄文版《阿基米德全集》，第一題就是阿基米德折弦定理．
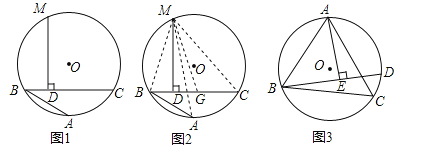
阿基米德折弦定理：如圖1，AB和BC是⊙O的兩條弦（即折線ABC是圓的一條折弦），BC＞AB，M是
的中點，則從M向BC所作垂線的垂足D是折弦ABC的中點，即CD=AB+BD．下面是運用“截長法”證明CD=AB+BD的部分證明過程．證明：如圖2，在CB上截取CG=AB，連接MA，MB，MC和MG．
∵M是的中點，∴MA=MC．
…
任務：
（1）請按照上面的證明思路，寫出該證明的剩余部分；
（2）填空：如圖3，已知等邊△ABC內(nèi)接于⊙O，AB=2，D為
上一點，∠ABD=45°，AE⊥BD于點E，則△BDC的周長是 ．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
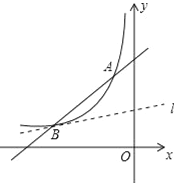
【題目】如圖，一次函數(shù)y=x+b的圖象與反比例函數(shù)
（k為常數(shù)，k≠0）的圖象交于點A（﹣1，4）和點B（a，1）．
（1）求反比例函數(shù)的表達式和a、b的值；
（2）若A、O兩點關于直線l對稱，請連接AO，并求出直線l與線段AO的交點坐標．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com