
【題目】如圖,直線y=﹣x+4分別交x軸、y軸于A、C兩點,拋物線y=﹣x2+mx+4經過點A,且與x軸的另一個交點為點B.連接BC,過點C作CD∥x軸交拋物線于點D

(1)求拋物線的函數表達式;
(2)若點E是拋物線上的點,求滿足∠ECD=∠BCO的點E的坐標;
(3)點M在y軸上且位于點C上方,點N在直線AC上,點P為第一象限內的拋物線上一點,若以點C、M、N、P為頂點的四邊形是菱形,求菱形的邊長.
【答案】(1)y=﹣x2+3x+4;(2)E的坐標為E![]() 或
或![]() ;(3)4
;(3)4![]() ﹣2或
﹣2或![]() .
.
【解析】
(1)利用直線方程求得點A、C的坐標,根據點A、C坐標求得拋物線解析式;
(2)分點E在CD上方、點E在CD下方兩種情況,分別求解即可;
(3)分CM為菱形的一條邊、CM為菱形的對角線兩種情況,分別求解即可.
解:(1)y=﹣x+4,令x=0,則y=4,令y=0,則x=4,

則點A、C的坐標分別為(4,0)、(0,4),
將點A的坐標代入拋物線的表達式并解得:m=3,
故拋物線的表達式為:y=﹣x2+3x+4①,
令y=0,則x=﹣1或4,故點B(﹣1,0);
(2)①當點E在CD上方時,

tan∠BCO=![]() ,
,
則直線CE的表達式為:y=![]() x+4②,
x+4②,
聯立①②并解得:x=0或![]() (舍去0),
(舍去0),
則點E(![]() ,
,![]() );
);
②當點E在CD下方時,
同理可得:點E′(![]() ,
,![]() );
);
故點E的坐標為E(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)①如圖2,當CM為菱形的一條邊時,
過點P作PQ∥x軸,∵OA=OC=4,
∴∠PMQ=∠CAO=45°,
設點P(x,﹣x2+3x+4),
則PM=![]() PQ=
PQ=![]() x,
x,
C、M、N、P為頂點的四邊形是菱形,則PM=PN,
即:![]() x=﹣x2+3x+4,解得:x=0或4﹣
x=﹣x2+3x+4,解得:x=0或4﹣![]() (舍去0),
(舍去0),
故菱形邊長為![]() x=4
x=4![]() ﹣2;
﹣2;
②如圖3,當CM為菱形的對角線時,
同理可得:菱形邊長為2![]() ;
;
故:菱形邊長為4![]() ﹣2或
﹣2或![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+2經過A(﹣1,0),B(2,0),C三點.直線y=mx+![]() 交拋物線于A,Q兩點,點P是拋物線上直線AQ上方的一個動點,作PF⊥x軸,垂足為F,交AQ于點N.
交拋物線于A,Q兩點,點P是拋物線上直線AQ上方的一個動點,作PF⊥x軸,垂足為F,交AQ于點N.

(1)求拋物線的解析式;
(2)如圖①,當點P運動到什么位置時,線段PN=2NF,求出此時點P的坐標;
(3)如圖②,線段AC的垂直平分線交x軸于點E,垂足為D,點M為拋物線的頂點,在直線DE上是否存在一點G,使△CMG的周長最小?若存在,請求出點G的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,反比例函數y=![]() (x>0)的圖象與邊長是6的正方形OABC的兩邊AB,BC分別相交于M,N 兩點,△OMN的面積為10.若動點P在x軸上,則PM+PN的最小值是( )
(x>0)的圖象與邊長是6的正方形OABC的兩邊AB,BC分別相交于M,N 兩點,△OMN的面積為10.若動點P在x軸上,則PM+PN的最小值是( )

A. 6![]() B. 10 C. 2
B. 10 C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,AC是直徑,點D是AC延長線上一點,且∠DBC=∠BAC,![]() .
.
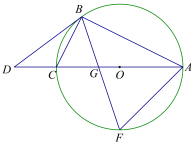
(1)求證:BD是⊙O的切線;(2)求![]() 的值;(3)如圖,直徑AC=5,
的值;(3)如圖,直徑AC=5,![]() ,求△ABF面積.
,求△ABF面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某鄉鎮實施產業扶貧,幫助貧困戶承包了荒山種植某種蘋果到了收獲季節,投入市場銷售時,調查市場行情,發現該蘋果的銷售不會虧本,且該產品的日銷售量y(千克)與銷售單價x(元)之間滿足一次函數關系關于銷售單價、日銷售量、日銷售利潤的幾組對應值如表:
銷售單價x(元) | 10 | 15 | 23 | 28 |
日銷售量y(千克) | 200 | 150 | 70 | m |
日銷售利潤w(元) | 400 | 1050 | 1050 | 400 |
(注:日銷售利潤=日銷售量×(銷售單價﹣成本單價))
(1)求y關于x的函數解析式(要寫出x的取值范圍)及m的值;
(2)根據以上信息,填空:產品的成本單價是 元,當銷售單價x= 元時,日銷售利潤w最大,最大值是 元;
(3)某農戶今年共采摘蘋果4800千克,該品種蘋果的保質期為40天,根據(2)中獲得最大利潤的方式進行銷售,能否銷售完這批蘋果?請說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了科學建設“學生健康成長工程”.隨機抽取了部分學生家庭對其家長進行了主題為“周末孩子在家您關心嗎?”的問卷調查,將回收的問卷進行分析整理,得到了如下的樣本統計表和扇形統計圖:
代號 | 情況分類 | 家庭數 |
| 帶孩子玩并且關心其作業完成情況 | 16 |
| 只關心其作業完成情況 | b |
| 只帶孩子玩 | 8 |
| 既不帶孩子玩也不關心其作業完成情況 | d |
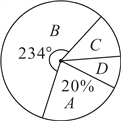
(1)求![]() 的值;
的值;
(2)該校學生家庭總數為500,學校決定按比例在![]() 類家庭中抽取家長組成培訓班,其比例為
類家庭中抽取家長組成培訓班,其比例為![]() 類取20%,
類取20%,![]() 類各取60%,請你估計該培訓班的家庭數;
類各取60%,請你估計該培訓班的家庭數;
(3)若在![]() 類家庭中只有一個城鎮家庭,其余是農村家庭,請用列舉法求出在
類家庭中只有一個城鎮家庭,其余是農村家庭,請用列舉法求出在![]() 類中隨機抽出2個家庭進行深度采訪,其中有一個是城鎮家庭的概率.
類中隨機抽出2個家庭進行深度采訪,其中有一個是城鎮家庭的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在矩形ABCD中,AB=6,BC=12,點E在邊BC上,且BE=2CE,將矩形沿過點E的直線折疊,點C,D的對應點分別為C′,D′,折痕與邊AD交于點F,當點B,C′,D′恰好在同一直線上時,AF的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有以下六個命題,①同旁內角互補;②若x2=4,則x=2;③![]() ;④平分弦的直徑垂直于弦;⑤等弧所對的圓心角相等;⑥相等的圓心角所對的弧相等.從這六個命題中隨機任意抽取一個命題是真命題的概率為_____.
;④平分弦的直徑垂直于弦;⑤等弧所對的圓心角相等;⑥相等的圓心角所對的弧相等.從這六個命題中隨機任意抽取一個命題是真命題的概率為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A. “買一張電影票,座位號為偶數”是必然事件
B. 若甲、乙兩組數據的方差分別為S甲2=0.3,S乙2=0.1,則甲組數據比乙組數據穩定
C. 一組數據2,4,5,5,3,6的眾數是5
D. 一組數據2,4,5,5,3,6的平均數是5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com