【題目】閱讀與應用：閱讀1：a、b為實數，且a＞0，b＞0，因為
，所以
從而
（當a=b時取等號）．
閱讀2：若函數
；（m＞0，x＞0，m為常數），由閱讀1結論可知：
，所以當
，即
時，函數的最小值為
．
閱讀理解上述內容，解答下列問題：
問題1：已知一個矩形的面積為4，其中一邊長為x，則另一邊長為
，周長為2（
），求當x= 時，周長的最小值為 ；
問題2：已知函數
（
）與函數
（），
當x= 時，
的最小值為 ；
問題3：某民辦學校每天的支出總費用包含以下三個部分：一是教職工工資4900元；二是學生生活費成本每人10元；三是其他費用．其中，其他費用與學生人數的平方成正比，比例系數為0.01．當學校學生人數為多少時，該校每天生均投入最低？最低費用是多少元？（生均投入=支出總費用÷學生人數）
【答案】（1）2，8；（2）2，6；（3）700，24．
【解析】
試題分析：問題1：由閱讀2得到
的范圍，進一步得到周長的最小值；
問題2：把
變形為
，由閱讀2得到的范圍，進一步即可求解；
問題3：可設學校學生人數為x人，根據生均投入=支出總費用÷學生人數，列出代數式，再由閱讀2得到范圍，從而求解．
試題解析：問題1：
（
），解得x=2，x=2時，有最小值為
=4．故當x=2時，周長的最小值為2×4=8；
問題2：∵
（
），
（），∴=，
，解得x=2，x=2時，有最小值為
=6；
問題3：設學校學生人數為x人，則生均投入=
=
=
，
（），解得x=700，x=700時，
有最小值為
=1400，故當x=700時，生均投入的最小值為10+0.01×1400=24元．
答：當學校學生人數為700時，該校每天生均投入最低，最低費用是24元．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖，AB∥CD，點E，F分別在AB，CD上，連接EF，∠AEF、∠CFE的平分線交于點G，∠BEF、∠DFE的平分線交于點H．
（1）求證：四邊形EGFH是矩形；
（2）小明在完成（1）的證明后繼續進行了探索，過G作MN∥EF，分別交AB，CD于點M，N，過H作PQ∥EF，分別交AB，CD于點P，Q，得到四邊形MNQP，此時，他猜想四邊形MNQP是菱形，請在下列框中補全他的證明思路．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀理解拋物線
上任意一點到點（0，1）的距離與到直線y=﹣1的距離相等，你可以利用這一性質解決問題．
問題解決
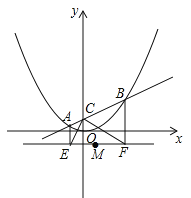
如圖，在平面直角坐標系中，直線
與y軸交于C點，與函數的圖象交于A，B兩點，分別過A，B兩點作直線y=﹣1的垂線，交于E，F兩點．
（1）寫出點C的坐標，并說明∠ECF=90°；
（2）在△PEF中，M為EF中點，P為動點．
①求證：
；
②已知PE=PF=3，以EF為一條對角線作平行四邊形CEDF，若1＜PD＜2，試求CP的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】定義：如圖1，點M，N把線段AB分割成AM，MN和BN，若以AM，MN，BN為邊的三角形是一個直角三角形，則稱點M，N是線段AB的勾股分割點．
（1）已知點M，N是線段AB的勾股分割點，若AM=2，MN=3，求BN的長；
（2）如圖2，在△ABC中，FG是中位線，點D，E是線段BC的勾股分割點，且EC＞DE≥BD，連接AD，AE分別交FG于點M，N，求證：點M，N是線段FG的勾股分割點；
（3）已知點C是線段AB上的一定點，其位置如圖3所示，請在BC上畫一點D，使點C，D是線段AB的勾股分割點（要求尺規作圖，保留作圖痕跡，畫一種情形即可）；
（4）如圖4，已知點M，N是線段AB的勾股分割點，MN＞AM≥BN，△AMC，△MND和△NBE均為等邊三角形，AE分別交CM，DM，DN于點F，G，H，若H是DN的中點，試探究
，
和
的數量關系，并說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com