
【題目】在平面直角坐標系中,拋物線![]() 與x軸交于A,B兩點(A在B的左側),與y軸交于點C,頂點為D.
與x軸交于A,B兩點(A在B的左側),與y軸交于點C,頂點為D.
(1)請直接寫出點A,C,D的坐標;
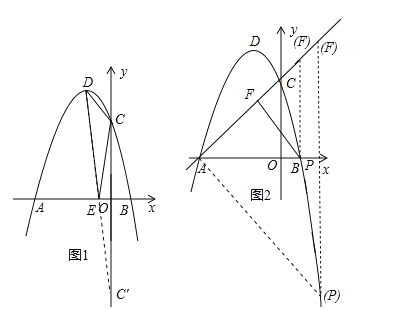
(2)如圖(1),在x軸上找一點E,使得△CDE的周長最小,求點E的坐標;
(3)如圖(2),F為直線AC上的動點,在拋物線上是否存在點P,使得△AFP為等腰直角三角形?若存在,求出點P的坐標,若不存在,請說明理由.
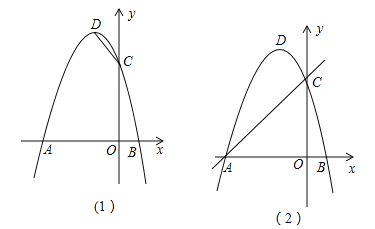
【答案】(1)A(﹣3,0),C(0,3),D(﹣1,4);(2)E(![]() ,0);(3)P(2,﹣5)或(1,0).
,0);(3)P(2,﹣5)或(1,0).
【解析】
試題分析:(1)令拋物線解析式中y=0,解關于x的一元二次方程即可得出點A、B的坐標,再令拋物線解析式中x=0求出y值即可得出點C坐標,利用配方法將拋物線解析式配方即可找出頂點D的坐標;
(2)作點C關于x軸對稱的點C′,連接C′D交x軸于點E,此時△CDE的周長最小,由點C的坐標可找出點C′的坐標,根據點C′、D的坐標利用待定系數法即可求出直線C′D的解析式,令其y=0求出x值,即可得出點E的坐標;
(3)根據點A、C的坐標利用待定系數法求出直線AC的解析式,假設存在,設點F(m,m+3),分∠PAF=90°、∠AFP=90°和∠APF=90°三種情況考慮.根據等腰直角三角形的性質結合點A、F點的坐標找出點P的坐標,將其代入拋物線解析式中即可得出關于m的一元二次方程,解方程求出m值,再代入點P坐標中即可得出結論.
試題解析:(1)當![]() 中y=0時,有
中y=0時,有![]() ,解得:
,解得:![]() =﹣3,
=﹣3,![]() =1,∵A在B的左側,∴A(﹣3,0),B(1,0).
=1,∵A在B的左側,∴A(﹣3,0),B(1,0).
當![]() 中x=0時,則y=3,∴C(0,3).
中x=0時,則y=3,∴C(0,3).
∵![]() =
=![]() ,∴頂點D(﹣1,4).
,∴頂點D(﹣1,4).
(2)作點C關于x軸對稱的點C′,連接C′D交x軸于點E,此時△CDE的周長最小,如圖1所示.
∵C(0,3),∴C′(0,﹣3).
設直線C′D的解析式為y=kx+b,則有:![]() ,解得:
,解得:![]() ,∴直線C′D的解析式為y=﹣7x﹣3,當y=﹣7x﹣3中y=0時,x=
,∴直線C′D的解析式為y=﹣7x﹣3,當y=﹣7x﹣3中y=0時,x=![]() ,∴當△CDE的周長最小,點E的坐標為(
,∴當△CDE的周長最小,點E的坐標為(![]() ,0).
,0).
(3)設直線AC的解析式為y=ax+c,則有:![]() ,解得:
,解得:![]() ,∴直線AC的解析式為y=x+3.
,∴直線AC的解析式為y=x+3.
假設存在,設點F(m,m+3),△AFP為等腰直角三角形分三種情況(如圖2所示):
①當∠PAF=90°時,P(m,﹣m﹣3),∵點P在拋物線![]() 上,∴
上,∴![]() ,解得:m1=﹣3(舍去),m2=2,此時點P的坐標為(2,﹣5);
,解得:m1=﹣3(舍去),m2=2,此時點P的坐標為(2,﹣5);
②當∠AFP=90°時,P(2m+3,0)
∵點P在拋物線![]() 上,∴
上,∴![]() ,解得:m3=﹣3(舍去),m4=﹣1,此時點P的坐標為(1,0);
,解得:m3=﹣3(舍去),m4=﹣1,此時點P的坐標為(1,0);
③當∠APF=90°時,P(m,0),∵點P在拋物線![]() 上,∴
上,∴![]() ,解得:m5=﹣3(舍去),m6=1,此時點P的坐標為(1,0).
,解得:m5=﹣3(舍去),m6=1,此時點P的坐標為(1,0).
綜上可知:在拋物線上存在點P,使得△AFP為等腰直角三角形,點P的坐標為(2,﹣5)或(1,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】已知O是直線AB上的一點,∠COD是直角,OE平分∠BOC.
(1)如圖①,若∠AOC=30°,求∠DOE的度數;
(2)在圖①中,若∠AOC= ![]() ,直接寫出∠DOE的度數(用含
,直接寫出∠DOE的度數(用含 ![]() 的代數式表示);
的代數式表示);
(3)將圖①中的∠DOC繞頂點O順時針旋轉至圖②的位置,探究∠AOC和∠DOE的度數之間的關系,寫出你的結論,并說明理由;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC和△A′B′C′關于直線m對稱。
(1)結合圖形指出對稱點.
(2)連接A、A′,直線m與線段AA′有什么關系?
(3)延長線段AC與A′C′,它們的交點與直線m有怎樣的關系?其它對應線段(或其延長線)的交點呢?你發現了什么規律,請敘述出來與同伴交流。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,線段AD、FC、EB兩兩相交,連接AB、CD、EF,則∠A+∠B+∠C+∠D+∠E+∠F=( ) 
A.360°
B.240°
C.200°
D.180°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點D是BC的中點,點E在AD上. 
(1)圖中的全等三角形有;
(2)從你找到的全等三角形中選出其中一對加以證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com