
【題目】已知A、B是數軸上的兩個點,點A表示的數為13,點B表示的數為-5,動點P從點B出發,以每秒4個單位長度的速度沿數軸向右勻速運動,設運動時間為![]() 秒.
秒.
(1)BP= ,點P表示的數 (分別用含![]() 的代數式表示);
的代數式表示);
(2)點P運動多少秒時,PB=2PA?
(3)若M為BP的中點,N為PA的中點,點P在運動的過程中,線段MN的長度是否發生變化?若變化,請說明理由;若不變,請求出線段MN的長.
【答案】(1)![]() ,
,![]() ;(2)3秒或9秒;(3)長度不發生變化,長度是9.
;(2)3秒或9秒;(3)長度不發生變化,長度是9.
【解析】試題分析:(1)根據BP=速度×時間可表示出BP的長,點P表示的數為-5+4t;
(2) 分點P在AB之間運動時和點P在運動到點A的右側時兩種情況列出方程求解即可;
(3) 分點P在AB之間運動時和點P在運動到點A的右側時兩種情況,利用中點的定義和線段的和差求出MN的長即可.
解:(1)由題意得,BP=4t,點P表示的數是-5+4t;
(2)當點P在AB之間運動時,由題意得,
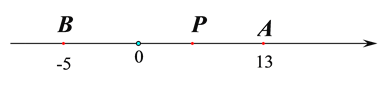
PB=4t,PA=13-(-5+4t)=18-4 t,
∵PB=2PA,
∴4t=2(18-4 t),
∴t=3;
當點P在運動到點A的右側時,由題意得,

PB=4t,PA=-5+4t-13=4 t -18,
∵PB=2PA,
∴4t=2(4 t -18),
∴t=9;
綜上可知,點P運動多3秒或9秒時,PB=2PA.
(3)當點P在AB之間運動時,由題意得,

PB=4t,PA=18-4 t,
∵M為BP的中點,N為PA的中點,
∴![]() ,
,![]() ,
,
∴MN=MP+NP=2t+9-2t=9;
當點P在運動到點A的右側時,由題意得,

PB=4t,PA=4 t -18,
∵M為BP的中點,N為PA的中點,
∴![]() ,
,![]() ,
,
∴MN=MP-NP=2t-(2t-9)=9;
綜上可知,線段MN的長度不發生變化,長度是9.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
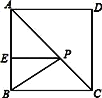
【題目】如圖,在正方形ABCD中,E是AB上一點,BE=2,AE=3,P是AC上一動點,則PB+PE的最小值是( ).
A. 5 B. 5![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,射線BC∥射線OA,∠C=∠BAO=100°,試回答下列問題:
(1)如圖①,求證:OC∥AB;
(2)若點E、F在線段BC上,且滿足∠EOB=∠AOB,并且OF平分∠BOC,
①如圖②,若∠AOB=30°,則∠EOF的度數等于多少(直接寫出答案即可);
②若平行移動AB,當∠BOC=6∠EOF時,求∠ABO.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AB為直徑的⊙O分別與BC,AC交于點D,E,過點D作⊙O的切線DF,交AC于點F. 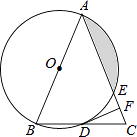
(1)求證:DF⊥AC;
(2)若⊙O的半徑為4,∠CDF=22.5°,求陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在邊長為4的正△ABC中,點P以每秒1cm的速度從點A出發,沿折線AB﹣BC運動,到點C停止.過點P作PD⊥AC,垂足為D,PD的長度y(cm)與點P的運動時間x(秒)的函數圖象如圖2所示.當點P運動5.5秒時,PD的長是( )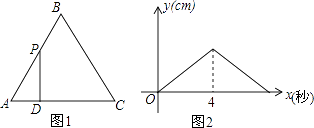
A.![]() cm
cm
B.![]() cm
cm
C.2 ![]() cm
cm
D.3 ![]() cm
cm
查看答案和解析>>
科目:初中數學 來源: 題型:
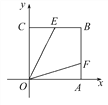
【題目】如圖,正方形OABC中,點B(4,4),點E,F分別在邊BC,BA上,OE=![]() ,若∠EOF=45°,則OF的解析式為 ( )
,若∠EOF=45°,則OF的解析式為 ( )
A. y=![]() x B. y=
x B. y=![]() x C. y=
x C. y=![]() x D. y=
x D. y=![]() x
x
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新華書店舉行購書優惠活動
①一次性購書不超過100元,不享受打折優惠
②一次性購書超過100元但不超過200元一律打九折;
③一次性購書200元以上一律打七折
小麗在這次活動中,兩次購書總共付款240.87元,第二次購書原價是第一次購書原價的3倍,那么小麗這兩次購書原價的總和是_____元.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com