
【題目】某中學計劃購買A型和B型課桌凳共200套.經招標,購買一套A型課桌凳比購買一套B型課桌凳少用40元,且購買4套A型和5套B型課桌凳共需1820元.
(1)求購買一套A型課桌凳和一套B型課桌凳各需多少元?
(2)學校根據實際情況,要求購買這兩種課桌凳總費用不能超過40880元,并且購買A型課桌凳的數量不能超過B型課桌凳數量的 ![]() ,求該校本次購買A型和B型課桌凳共有幾種方案?哪種方案的總費用最低?
,求該校本次購買A型和B型課桌凳共有幾種方案?哪種方案的總費用最低?
【答案】
(1)解:設A型每套x元,則B型每套(x+40)元.
由題意得:4x+5(x+40)=1820.
解得:x=180,x+40=220.
即購買一套A型課桌凳和一套B型課桌凳各需180元、220元
(2)解:設購買A型課桌凳a套,則購買B型課桌凳(200﹣a)套.
由題意得:  ,
,
解得:78≤a≤80.
∵a為整數,
∴a=78、79、80.
∴共有3種方案,
設購買課桌凳總費用為y元,
則y=180a+220(200﹣a)=﹣40a+44000.
∵﹣40<0,y隨a的增大而減小,
∴當a=80時,總費用最低,此時200﹣a=120,
即總費用最低的方案是:購買A型80套,購買B型120套
【解析】(1)根據購買一套A型課桌凳比購買一套B型課桌凳少用40元,以及購買4套A型和5套B型課桌凳共需1820元,得出等式方程求出即可;(2)利用要求購買這兩種課桌凳總費用不能超過40880元,并且購買A型課桌凳的數量不能超過B型課桌凳數量的 ![]() ,得出不等式組,求出a的值即可,再利用一次函數的增減性得出答案即可.
,得出不等式組,求出a的值即可,再利用一次函數的增減性得出答案即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】在中俄“海上聯合﹣2014”反潛演習中,我軍艦A測得潛艇C的俯角為30°,位于軍艦A正上方1000米的反潛直升機B測得潛艇C的俯角為68°,試根據以上數據求出潛艇C離開海平面的下潛深度.(結果保留整數,參考數據:sin68°≈0.9,cos68°≈0.4,tan68°≈2.5, ![]() 1.7)
1.7)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了加強訓練學生的籃球和足球運球技能,準備購買一批籃球和足球用于訓練,已知1個籃球和2個足球共需116元;2個籃球和3個足球共需204元
![]() 求購買1個籃球和1個足球各需多少元?
求購買1個籃球和1個足球各需多少元?
![]() 若學校準備購進籃球和足球共40個,并且總費用不超過1800元,則籃球最多可購買多少個?
若學校準備購進籃球和足球共40個,并且總費用不超過1800元,則籃球最多可購買多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3.點D是BC邊上的一動點(不與點B、C重合),過點D作DE⊥BC交AB于點E,將∠B沿直線DE翻折,點B落在射線BC上的點F處.當△AEF為直角三角形時,BD的長為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,鈍角△ABC.

(1)過A作AE⊥BC,過B作BF⊥AC,垂足分別為E,F,AE,BF相交于H;
(2)過A作AM∥BC,過B作BM∥AC,相交于M;
(3)若∠AMB=115°,求∠AHB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC的周長是20,三邊分別為a,b,c.
(1)若b是最大邊,求b的取值范圍;
(2)若△ABC是三邊均不相等的三角形,b是最大邊,c是最小邊,且b=3c,a,b,c均為整數,求△ABC的三邊長.
查看答案和解析>>
科目:初中數學 來源: 題型:
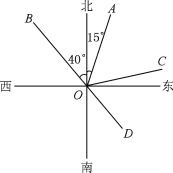
【題目】如圖,射線OA表示的方向是北偏東15°,射線OB表示的方向是北偏西40°.
(1)若∠AOC=∠AOB,則射線OC表示的方向是 ;
(2)若射線OD是射線OB的反向延長線,則射線OD表示的方向是 ;
(3)∠BOD可以看作是由OB繞點O逆時針方向旋轉至OD形成的角,作∠BOD的平分線OE;
(4)在(1),(2),(3)的條件下,求∠COE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,AB=AC,點D在底邊BC上,添加下列條件后,仍無法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料: 如圖1,在平面直角坐標系xOy中,直線y1=ax+b與雙曲線y2= ![]() 交于A(1,3)和B(﹣3,﹣1)兩點.
交于A(1,3)和B(﹣3,﹣1)兩點.
觀察圖象可知:
①當x=﹣3或1時,y1=y2;
②當﹣3<x<0或x>1時,y1>y2 , 即通過觀察函數的圖象,可以得到不等式ax+b> ![]() 的解集.
的解集.
有這樣一個問題:求不等式x3+4x2﹣x﹣4>0的解集.
某同學根據學習以上知識的經驗,對求不等式x3+4x2﹣x﹣4>0的解集進行了探究.
下面是他的探究過程,請將探究過程補充完整:
將不等式按條件進行轉化:
當x=0時,原不等式不成立;
當x>0時,原不等式可以轉化為x2+4x﹣1> ![]() ;
;
當x<0時,原不等式可以轉化為x2+4x﹣1< ![]() ;
;
(1)構造函數,畫出圖象 設y3=x2+4x﹣1,y4= ![]() ,在同一坐標系中分別畫出這兩個函數的圖象.
,在同一坐標系中分別畫出這兩個函數的圖象.
雙曲線y4= ![]() 如圖2所示,請在此坐標系中畫出拋物線y3=x2+4x﹣1;(不用列表)
如圖2所示,請在此坐標系中畫出拋物線y3=x2+4x﹣1;(不用列表)
(2)確定兩個函數圖象公共點的橫坐標 觀察所畫兩個函數的圖象,猜想并通過代入函數解析式驗證可知:滿足y3=y4的所有x的值為;
(3)借助圖象,寫出解集 結合(1)的討論結果,觀察兩個函數的圖象可知:不等式x3+4x2﹣x﹣4>0的解集為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com