
【題目】如圖1,直線MN與直線AB、CD分別交于點E、F,∠1與∠2互補.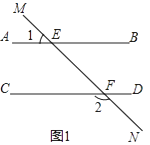
(1)試判斷直線AB與CD的位置關系,并說明理由;
(2)如圖2,∠AEF與∠EFC的角平分線交于點P,PF∥GH,求證:GH⊥EG;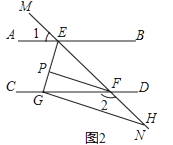
(3)如圖3,在(2)的條件下,連接PH,K是GH上一點使∠PHK=∠HPK,作PQ平分∠EPK,問∠HPQ的大小是否發生變化?若不變,請求出其值;若變化,說明理由.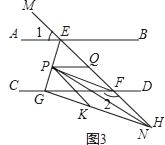
【答案】
(1)解:∵∠1+∠AEF=180°,
∠1+∠2=180°,
∴∠AEF=∠2,
∴AB∥CD.
(2)解:∵AB∥CD,
∴∠AEF+∠EFC=180°;
∵∠AEF與∠EFC的角平分線交于點P,
∴∠PEF+∠PFE=90°,即PF⊥GE;
∵PF∥GH,
∴GH⊥EG
(3)解:∵PF∥GH,
∴∠FPH=∠PHK,而∠PHK=∠HPK,
∴∠FPH=∠KPH(設為α);
∵PQ平分∠EPK,
∴∠KPQ= ![]() =45°+α,
=45°+α,
∴∠HPQ=45°+α﹣α=45°,
即∠HPQ的大小不會發生變化
【解析】掌握對頂角的性質以及平行線的判定定理進行解決實際問題.
【考點精析】本題主要考查了平行線的判定與性質的相關知識點,需要掌握由角的相等或互補(數量關系)的條件,得到兩條直線平行(位置關系)這是平行線的判定;由平行線(位置關系)得到有關角相等或互補(數量關系)的結論是平行線的性質才能正確解答此題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
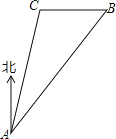
【題目】如圖,在小島上有一觀測站A,燈塔B在觀測站A北偏東45°的方向.燈塔C在燈塔B的正西方向,且相距10海里,燈塔C與觀測站A相距![]() 海里,請你測算燈塔C處在觀測站A的什么方向?
海里,請你測算燈塔C處在觀測站A的什么方向?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表是我市某一天在不同時段測得的氣溫情況
0:00 | 4:00 | 8:00 | 12:00 | 16:00 | 20:00 |
25℃ | 27℃ | 29℃ | 32℃ | 34℃ | 30℃ |
則這一天氣溫的極差是℃.
查看答案和解析>>
科目:初中數學 來源: 題型:
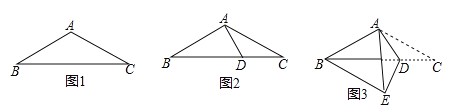
【題目】如圖1,在等腰三角形ABC中,AB=AC=4,BC=7.如圖2,在底邊BC上取一點D,連結AD,使得∠DAC=∠ACD.如圖3,將△ACD沿著AD所在直線折疊,使得點C落在點E處,連結BE,得到四邊形ABED.則BE的長是( )
A.4 B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
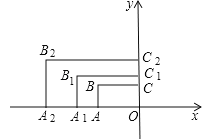
【題目】如圖,在平面直角坐標系中,矩形AOCB的兩邊OA、OC分別在x軸和y軸上,且OA=2,OC=1.在第二象限內,將矩形AOCB以原點O為位似中心放大為原來的![]() 倍,得到矩形A1OC1B1,再將矩形A1OC1B1以原點O為位似中心放大
倍,得到矩形A1OC1B1,再將矩形A1OC1B1以原點O為位似中心放大![]() 倍,得到矩形A2OC2B2…,以此類推,得到的矩形AnOCnBn的對角線交點的坐標為 .
倍,得到矩形A2OC2B2…,以此類推,得到的矩形AnOCnBn的對角線交點的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,某溫室屋頂結構外框為△ABC,立柱AD垂直平分橫梁BC,∠B=30°,斜梁AC=4m,為增大向陽面的面積,將立柱AD增高并改變位置后變為EF,使屋頂結構外框由△ABC變為△EBC(點E在BA的延長線上)如圖2所示,且立柱EF⊥BC,若EF=3m,則斜梁增加部分AE的長為m. 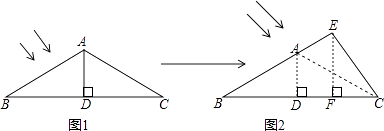
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com