
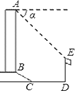
【題目】如圖,某辦公大樓正前方有一根高度是15米的旗桿ED,從辦公大樓頂端A測得旗桿頂端E的俯角α是45°,旗桿底端D到大樓前梯坎底邊的距離DC是20米,梯坎坡長BC是12米,梯坎坡度i=1:![]() ,則大樓AB的高度為________米.(精確到0.1米,參考數據:
,則大樓AB的高度為________米.(精確到0.1米,參考數據:![]() ,
,![]() ,
,![]() )
)
【答案】6![]() +29
+29
【解析】
延長AB交DC于H,作EG⊥AB于G,則GH=DE=15米,EG=DH,設BH=x米,則CH=![]() x米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6
x米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6![]() 米,得出BG、EG的長度,證明△AEG是等腰直角三角形,得出AG=EG=6
米,得出BG、EG的長度,證明△AEG是等腰直角三角形,得出AG=EG=6![]() +20(米),即可得出大樓AB的高度.
+20(米),即可得出大樓AB的高度.
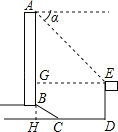
延長AB交DC于H,作EG⊥AB于G,如圖所示:
則GH=DE=15米,EG=DH,
∵梯坎坡度i=1:![]() ,
,
∴BH:CH=1:![]() ,
,
設BH=x米,則CH=![]() x米,
x米,
在Rt△BCH中,BC=12米,
由勾股定理得:x2+(![]() x)2=122,
x)2=122,
解得:x=6,
∴BH=6米,CH=6![]() 米,
米,
∴BG=GH﹣BH=15﹣6=9(米),EG=DH=CH+CD=6![]() +20(米),
+20(米),
∵∠α=45°,
∴∠EAG=90°﹣45°=45°,
∴△AEG是等腰直角三角形,
∴AG=EG=6![]() +20(米),
+20(米),
∴AB=AG+BG=6![]() +20+9=(6
+20+9=(6![]() +29)m.
+29)m.
故答案為:6![]() +29.
+29.


科目:初中數學 來源: 題型:
【題目】體育課上,小明、小強、小華三人在學習訓練踢足球,足球從一人傳到另一人就記為踢一次.
(1)如果從小強開始踢,經過兩次踢后,用樹狀圖表示或列表法求足球踢到了小華處的概率是多少
(2)如果從小明開始踢,經過踢三次后,球踢到了小明處的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】建華區對參加![]() 年中考的
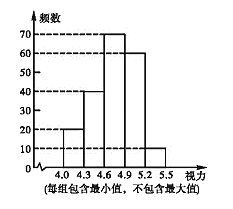
年中考的![]() 名初中畢業生進行了一次視力抽樣調查,繪制出頻數分布表和頻數分布直方圖的一部分.請根據圖、表信息解答下列問題:
名初中畢業生進行了一次視力抽樣調查,繪制出頻數分布表和頻數分布直方圖的一部分.請根據圖、表信息解答下列問題:
(1)在頻數分布表中,![]() 的值為 ,
的值為 ,![]() 的值為 ,并將頻數分布直方圖補充完整;
的值為 ,并將頻數分布直方圖補充完整;
(2)甲同學說:“我的視力情況是此次抽樣調查所得數據的中位數”,問甲同學的視力情況應在什么范圍?
(3)若視力在![]() 以上(含
以上(含![]() )均屬正常,則視力正常的人數占被統計人數的百分比是 ,并根據上述信息估計全區初中畢業生中視力正常的學生有多少人?
)均屬正常,則視力正常的人數占被統計人數的百分比是 ,并根據上述信息估計全區初中畢業生中視力正常的學生有多少人?
視力 | 頻數 | 頻率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“守護碧水藍天,守護我們的家園”,某市為了改善城市環境,預算 116 萬元購進 A、B 兩種型號的清掃機,已知 A 型號清掃機的單價比 B 型號清掃 機單價的 ![]() 多 1.2 萬元,若購進 2 臺 A 型號清掃機和 3 臺 B 型號清掃機花費 54.6 萬元.
多 1.2 萬元,若購進 2 臺 A 型號清掃機和 3 臺 B 型號清掃機花費 54.6 萬元.
(1)求 A 型號清掃機和 B 型號清掃機的單價分別為多少萬元;
(2)該市通過考察決定先購進兩種型號的清掃機共 10 臺,且 B 型號的清掃機 數量不能少于 A 型號清掃機的 1.5 倍,該市怎樣購買才能花費最少?最少花費 多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
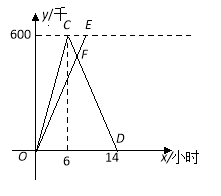
【題目】A,B兩城相距600千米,甲、乙兩車同時從A城出發駛向B城,甲車到達B城后立即返回.如圖是它們離A城的距離y(千米)與行駛時間 x(小時)之間的函數圖象.
(1)求甲車行駛過程中y與x之間的函數解析式,并寫出自變量x的取值范圍;
(2)當它們行駛了7小時時,兩車相遇,求乙車的速度及乙車行駛過程中y與x之間的函數解析式,并寫出自變量x的取值范圍;
(3)當兩車相距100千米時,求甲車行駛的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了抗擊新冠病毒疫情,全國人民眾志成城,守望相助.春節后某地一水果購銷商安排15輛汽車裝運A,B,C三種水果120噸銷售,所得利潤全部捐贈湖北抗疫.已知按計劃15輛汽車都要裝滿且每輛汽車只能裝同一種水果,每種水果所用車輛均不少于3輛,汽車對不同水果的運載量和每噸水果銷售獲利情況如下表.
水果品種 | A | B | C |
汽車運載量(噸/輛) | 10 | 8 | 6 |
水果獲利(元/噸) | 800 | 1200 | 1000 |
(1)設裝運A種水果的車輛數為x輛,裝運B種水果車輛數為y輛,根據上表提供的信
息,
①求y與x之間的函數關系式;
②設計車輛的安排方案,并寫出每種安排方案;
(2)若原有獲利不變的情況下,當地政府按每噸50元的標準實行運費補貼,該經銷商打算將獲利連同補貼全部捐出.問應采用哪種車輛安排方案,可以使這次捐款數w(元)最大化?捐款w(元)最大是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
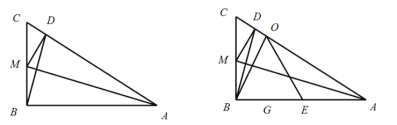
【題目】如圖,已知:在直角![]() 中,
中,![]() ,點
,點![]() 在邊
在邊![]() 上,且
上,且![]() 如果將
如果將![]() 沿
沿![]() 所在的直線翻折,點
所在的直線翻折,點![]() 恰好落在邊
恰好落在邊![]() 上的點
上的點![]() 處,點
處,點![]() 為
為![]() 邊上的一個動點,聯結
邊上的一個動點,聯結![]() ,以
,以![]() 圓心,
圓心,![]() 為半徑作⊙
為半徑作⊙![]() ,交線段
,交線段![]() 于點
于點![]() 和點
和點![]() ,作
,作![]() 交⊙
交⊙![]() 于點
于點![]() ,
,![]() 交線段
交線段![]() 于點
于點![]() .
.
(1)求點![]() 到點
到點![]() 和直線
和直線![]() 的距離
的距離
(2)如果點![]() 平分劣弧
平分劣弧![]() ,求此時線段
,求此時線段![]() 的長度
的長度
(3)如果![]() 為等腰三角形,以
為等腰三角形,以![]() 為圓心的⊙
為圓心的⊙![]() 與此時的⊙
與此時的⊙![]() 相切,求⊙
相切,求⊙![]() 的半徑
的半徑
查看答案和解析>>
科目:初中數學 來源: 題型:
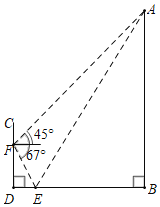
【題目】為了測量豎直旗桿AB的高度,某綜合實踐小組在地面D處豎直放置標桿CD,并在地面上水平放置一個平面鏡E,使得B,E,D在同一水平線上(如圖所示).該小組在標桿的F處通過平面鏡E恰好觀測到旗桿頂A(此時∠AEB=∠FED),在F處測得旗桿頂A的仰角為45°,平面鏡E的俯角為67°,測得FD=2.4米.求旗桿AB的高度約為多少米?(結果保留整數,參考數據:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于任意的實數m,n,定義運算“∧”,有m∧n=![]() .
.
(1)計算:3∧(-1);
(2)若![]() ,
,![]() ,求m∧n (用含x的式子表示);
,求m∧n (用含x的式子表示);
(3)若![]() ,
,![]() , m∧n=-2 ,求x的值 .
, m∧n=-2 ,求x的值 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com