
【題目】在平面直角坐標(biāo)系中,點![]() 為原點,點
為原點,點![]() 的坐標(biāo)為
的坐標(biāo)為![]() .如圖
.如圖![]() ,正方形
,正方形![]() 的頂點
的頂點![]() 在
在![]() 軸的負(fù)半軸上,點
軸的負(fù)半軸上,點![]() 在第二象限.現(xiàn)將正方形
在第二象限.現(xiàn)將正方形![]() 繞點
繞點![]() 順時針旋轉(zhuǎn)角
順時針旋轉(zhuǎn)角![]() 得到正方形
得到正方形![]() .
.
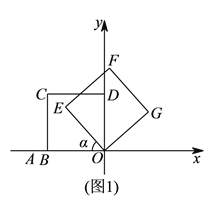

(![]() )如圖
)如圖![]() ,若
,若![]() ,
, ![]() ,求直線
,求直線![]() 的函數(shù)表達(dá)式.
的函數(shù)表達(dá)式.
(![]() )若
)若![]() 為銳角,
為銳角, ![]() ,當(dāng)
,當(dāng)![]() 取得最小值時,求正方形
取得最小值時,求正方形![]() 的面積.
的面積.
(![]() )當(dāng)正方形
)當(dāng)正方形![]() 的頂點
的頂點![]() 落在
落在![]() 軸上時,直線
軸上時,直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,
, ![]() 的其中兩邊之比能否為
的其中兩邊之比能否為![]() ?若能,求出
?若能,求出![]() 的坐標(biāo);若不能,試說明理由.
的坐標(biāo);若不能,試說明理由.
【答案】(1)直線![]() 的函數(shù)表達(dá)式為
的函數(shù)表達(dá)式為![]() ;
;
(2)![]() ;
;
(3)能,點![]() 的坐標(biāo)可為
的坐標(biāo)可為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
【解析】試題分析:(1)先判斷出△AEO為正三角形,再根據(jù)銳角三角函數(shù)求出OM即可;(2)判斷出當(dāng)AE⊥OQ時,線段AE的長最小,用勾股定理計算即可;(3)由△OEP的其中兩邊之比為![]() :1分三種情況進(jìn)行計算即可.
:1分三種情況進(jìn)行計算即可.
試題解析:(![]() )過點
)過點![]() 作
作![]() 于點
于點![]() ,
, ![]() 與
與![]() 軸交點為
軸交點為![]() ,
,
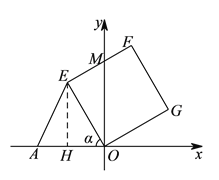
∵![]() ,
, ![]() ,
,
∴![]() 為正三角形,
為正三角形,
∴![]() ,
, ![]() ,
,
∴![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,
![]() ,即
,即![]() ,
,
∴![]() ,
,
∴點![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
設(shè)直線![]() 的函數(shù)表達(dá)式為
的函數(shù)表達(dá)式為![]() ,
,
把![]() 代入,
代入,
得![]() ,解得
,解得![]() ,
,
∴直線![]() 的函數(shù)表達(dá)式為
的函數(shù)表達(dá)式為![]() .
.
(![]() )當(dāng)
)當(dāng)![]() 時,線段
時,線段![]() 的長最小,
的長最小,
在![]() 中,
中,
![]() ,
,
即![]() ,
,
由勾股定理得![]() ,
,
即![]() ,
,
解得![]() ,
,
![]() ,
,
此時, 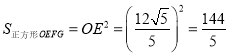 .
.
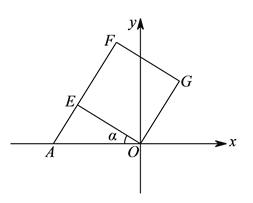
(![]() )能,
)能,
∵四邊形![]() 是正方形,
是正方形,
∴![]() ,
,
![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
①當(dāng)![]() 與
與![]() 重合時,
重合時, ![]() 是等腰直角三角形(如圖
是等腰直角三角形(如圖![]() )
)
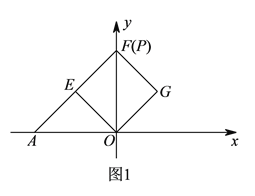
∴![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 坐標(biāo)為
坐標(biāo)為![]() .
.
當(dāng)減小正方形的邊長時,點![]() 在邊
在邊![]() 上,
上,
![]() 的其中兩邊之比不可能為
的其中兩邊之比不可能為![]() ,
,
當(dāng)增加正方形的邊長時,存在![]() (如圖
(如圖![]() )
)
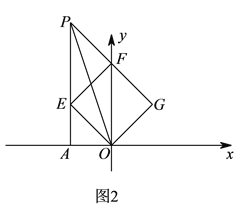
和![]() (如圖
(如圖![]() )兩種情況.
)兩種情況.
②如圖![]() 所示,當(dāng)
所示,當(dāng)![]() 時,
時,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,即
,即![]() .
.
在![]() 中,
中,
∵![]() ,
,
∴![]() 為等腰直角三角形,
為等腰直角三角形,
∵![]() ,
,
![]() ,
,
即![]() .
.
![]() ,
,
此時點![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
③如圖![]() 所示,當(dāng)
所示,當(dāng)![]() 時,過
時,過![]() 作
作![]() 軸于點
軸于點![]() ,
,
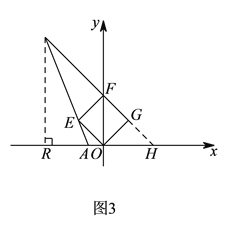
延長![]() 交
交![]() 軸于點
軸于點![]() .
.
∴![]() ,
,
![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
設(shè)正方形邊長為![]() ,
, ![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
又∵![]() ,
,
![]() ,
,
在![]() 中,由勾股定理得,
中,由勾股定理得,
![]() ,即
,即![]() ,
,
∴![]() ,得
,得![]() ,
,
![]() ,即
,即![]() .
.
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
![]() ,
,
即![]() ,
,
又∵在![]() 中,
中, ![]() ,
,
∴![]() ,
, ![]() .
.
∵![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
則![]() ,
,
此時點![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
④如圖![]() 所示,當(dāng)
所示,當(dāng)![]() 與
與![]() 重合時,
重合時, ![]() 是等腰直角三角形,
是等腰直角三角形,
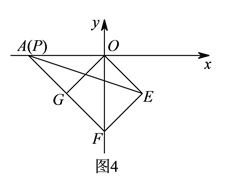
![]() ,
,
即![]() 滿足條件,此時點
滿足條件,此時點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,
在圖![]() 的基礎(chǔ)上,當(dāng)正方形的邊長減小時,
的基礎(chǔ)上,當(dāng)正方形的邊長減小時,
![]() 的其中兩邊之比不可能為
的其中兩邊之比不可能為![]() ,
,
當(dāng)正方形的邊長增加時,存在![]() (圖
(圖![]() )
)
⑤如圖![]() 所示,當(dāng)
所示,當(dāng)![]() 時,過
時,過![]() 作
作![]() 軸于點
軸于點![]() ,
,

記直線![]() 交
交![]() 軸于點
軸于點![]() ,
,
設(shè)正方形的邊長為![]() ,
, ![]() ,則
,則![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
∵![]() ,
,
![]() 即
即![]() ,
,
得![]() ,
,
![]() ,
,
在![]() 中,
中,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,則
,則![]() ,
,
四邊形![]() 是正方形,
是正方形,
∴![]() 即
即![]() ,
,
![]() 又
又![]() ,
,
∴![]() ,
,
![]() ,即
,即![]() ,
,
則![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,解得
,解得![]() ,
,
即![]() .
.
![]() 且
且![]() ,
,
∴![]() 為等腰直角三角形,∴
為等腰直角三角形,∴![]() ,
,
![]() ,此時點
,此時點![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,
綜上所述,點![]() 的坐標(biāo)可為
的坐標(biāo)可為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.


 亮點激活精編提優(yōu)100分大試卷系列答案
亮點激活精編提優(yōu)100分大試卷系列答案科目:初中數(shù)學(xué) 來源: 題型:
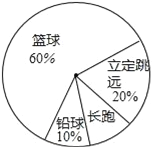
【題目】某班同學(xué)響應(yīng)“陽光體育運動”號召,利用課外活動積極參加體育鍛煉,每位同學(xué)從長跑、鉛球、立定跳遠(yuǎn)、籃球定時定點投籃中任選一項進(jìn)行了訓(xùn)練,訓(xùn)練前后都進(jìn)行了測試,現(xiàn)將項目選擇情況及訓(xùn)練后籃球定時定點投籃進(jìn)球數(shù)(每人投10次)進(jìn)行整理,作出如下統(tǒng)計圖表.
進(jìn)球數(shù)(個) | 8 | 7 | 6 | 5 | 4 | 3 |
人數(shù) | 2 | 1 | 4 | 7 | 8 | 2 |
請你根據(jù)圖表中的信息回答下列問題:
(1)訓(xùn)練后籃球定時定點投籃人均進(jìn)球數(shù)為 個;進(jìn)球數(shù)的中位數(shù)為 個,眾數(shù)為 個;
(2)該班共有多少學(xué)生;
(3)根據(jù)測試資料,參加籃球定時定點投籃的學(xué)生訓(xùn)練后比訓(xùn)練前的人均進(jìn)球增加了20%,求參加訓(xùn)練之前的人均進(jìn)球數(shù)(保留一位小數(shù)).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
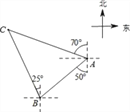
【題目】如圖,輪船在A處觀測燈塔C位于北偏西70°方向上,輪船從A處以每小時20海里的速度沿南偏西50°方向勻速航行,1小時后到達(dá)碼頭B處,此時,觀測燈塔C位于北偏西25°方向上,則燈塔C與碼頭B的距離是( )
A. 10![]() 海里 B. 10
海里 B. 10![]() 海里 C. 10
海里 C. 10![]() 海里 D. 20
海里 D. 20![]() 海里
海里
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC中,∠A=40°,AB的垂直平分線MN交AC于點D,∠DBC=30°,若AB=m,BC=n,則△DBC的周長為( )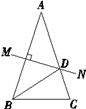
A.m+n
B.2m+n
C.m+2n
D.2m -n
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1是一個正三角形,分別連接這個正三角形各邊上的中點得到圖2,再連接圖2中間的小三角形各邊上的中點得到圖3,按此方法繼續(xù)下去.前三個圖形中三角形的個數(shù)分別是1個,5個,9個,那么第5個圖形中三角形的個數(shù)是個;第n個圖形中三角形的個數(shù)是個.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列函數(shù)關(guān)系中,屬于正比例函數(shù)關(guān)系的是( )
A.圓的面積與它的半徑
B.面積為常數(shù)S時矩形的長y與寬x
C.路程是常數(shù)時,行駛的速度v與時間t
D.三角形的底邊是常數(shù)a時它的面積S與這條邊上的高h
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com