
【題目】如圖,直角坐標系中,△ABC的頂點都在網格點上,其中,C點坐標為(1,2).
(1)寫出點A、B的坐標;
(2)將△ABC先向左平移2個單位長度,再向上平移1個單位長度,得到△A′B′C′,寫出A′B′C′的三個頂點坐標;
(3)求△ABC的面積.

【答案】(1)A(2,﹣1)、B(4,3);(2)A′(0,0)、B′(2,4)、C′(﹣1,3);(3)5.
【解析】
(1)A在第四象限,橫坐標為正,縱坐標為負;B的第一象限,橫縱坐標均為正;
(2)讓三個點的橫坐標減2,縱坐標加1即為平移后的坐標;
(3)△ABC的面積等于邊長為3,4的長方形的面積減去2個邊長為1,3和一個邊長為2,4的直角三角形的面積,把相關數值代入即可求解.
(1)寫出點A、B的坐標:A(2,﹣1)、B(4,3)
(2)將△ABC先向左平移2個單位長度,再向上平移1個單位長度,得到△A′B′C′,則A′B′C′的三個頂點坐標分別是A′(0,0)、B′(2,4)、C′(﹣1,3).
(3)△ABC的面積![]()


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,以點A為圓心,AB長為半徑畫弧,交CD于點E,連接AE、BE.作BF⊥AE于點F. 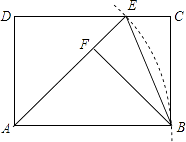
(1)求證:BF=AD;
(2)若EC= ![]() ﹣1,∠FEB=67.5°,求扇形ABE的面積(結果保留π).
﹣1,∠FEB=67.5°,求扇形ABE的面積(結果保留π).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛公交車從A站出發勻速開往B站.在行駛時間相同的前提下,如果車速是60千米/小時,就會超過B站0.2千米;如果車速是50千米/小時,就還需行駛0.8千米才能到達B站.
(1)求A站和B站相距多少千米?行駛時間是多少?如果要在行駛時間點恰好到達B站,行駛的速度是多少?
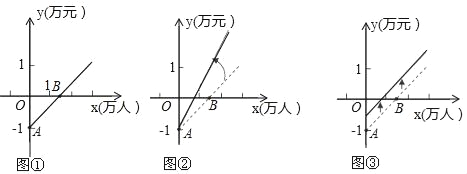
(2)圖①是這輛公交車線路的收支差額y(票價總收入減去運營成本)與乘客數量的函數圖象.目前這條線路虧損,為了扭虧,有關部門舉行了提高票價的聽證會.乘客代表認為:公交公司應節約能源,改善管理,降低運營成本,以此舉實現扭虧.公交公司認為:運營成本難以下降,公司己盡力,提高票價才能扭虧.根據這兩種意見,可以把圖①分別改畫成圖②和圖③.
(a)說明圖①中點A和點B的實際意義;
(b)你認為圖②和圖③兩個圖象中,反映乘客意見的是 ,反映公交公司意見的是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程或方程組解應用題:
某校初二年級的同學乘坐大巴車去北京展覽館參觀“砥礪奮進的五年”大型成就展,北京展覽館距離該校12千米,1號車出發3分鐘后,2號車才出發,結果兩車同時到達,已知2號車的平均速度是1號車的平均速度的1.2倍,求2號車的平均速度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,O為直線AB上一點,∠AOC=50°,OD平分∠AOC,OD⊥OE.
(1)請你數一數,圖中有多少個角?(備注:小于平角的角);
(2)請通過計算說明OE是否平分∠BOC.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形紙片ABCD中,AB=4,BC=8,將紙片沿EF折疊,使點C與點A重合,則下列結論錯誤的是( ) 
A.AF=AE
B.△ABE≌△AGF
C.EF=2 ![]()
D.AF=EF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)-102n×100×(-10)2n-1;
(2)[(-a)·(-b)2·a2b3c]2;
(3)(x3)2÷x2÷x-x3÷(-x)4·(-x4);
(4)(-9)3×![]() ×
×![]() ;
;
(5)xn+1·xn-1·x÷xm;
(6)a2·a3-(-a2)3-2a·(a2)3-2[(a3)3÷a3].
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義一種“十位上的數字比個位、百位上的數字都要小”的三位數叫做“V數”如“947”就是一個“V數”.若十位上的數字為2,則從1,3,4,5中任選兩數,能與2組成“V數”的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com