【題目】如圖，矩形ABCD中，AB=1，BC=2，BC在x軸上，一次函數y=kx﹣2的圖象經過點A、C，并與y軸交于點E，反比例函數y= 
的圖象經過點A．
（1）點E的坐標是；
（2）求反比例函數的解析式；
（3）求當一次函數的值小于反比例函數的值時，x的取值范圍．
【答案】
（1）E（0,﹣2）
（2）解：把C（4，0）代入y=kx﹣2得4k﹣2=0，解得k= 
，
∴一次函數解析式為y= x﹣2；
∵OC=4，
∴A點坐標為（6，1），
把A（6，1）代入y= 
得m=6×1=6，
∴反比例函數解析式為y= 
（3）解：令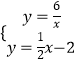 
解得 
，
∴另一個交點（﹣2，﹣3），
∴觀察圖象得：當x＜﹣2或 0＜x＜6時次函數的值小于反比例函數的值
【解析】解：（1）一次函數y=kx﹣2中令x=0得y=﹣2，
所以E（0，﹣2）；
（1）把x=0代入求出y的值，即可得E的坐標；
（2）利用待定系數法求出一次函數解析式，從而求出A的坐標，再由待定系數法求出反比例函數的解析式；
（3）把兩個函數的解析式聯立求出交點坐標，再結合圖像可得答案.
走進文言文系列答案科目：初中數學 來源： 題型：
【題目】在△ABC中，AB＝AC，∠BAC＝50° ，D是BC的中點，以AC為腰向外作等腰直角△ACE，∠EAC＝90°，連接BE，交AD于點F，交AC于點G．
（1）求∠AEB的度數；
（2）求證：∠AEB＝∠ACF；
（3）若AB＝4，求
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察下列圖形，并閱讀相關文字．
2條直線相交，3條直線相交，4條直線相交，5條直線相交；
有2對對頂角，有6對對頂角，有12對對頂角，有20對對頂角；
通過閱讀分析上面的材料，計算后得出規律，當n條直線相交于一點時，有多少對對頂角出現（n為大于2的整數）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，∠B=90°，AB∥ED ,交BC于E，交 AC于F， DE = BC,
.
（1） 求證：△FCD 是等腰三角形
（2） 若AB=3.5cm,求CD的長。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點
是等邊
內一點，
，
．以
為一邊作等邊三角形
，連接
、
．
（1）若
，判斷
_______
(填“
，
或
”)
（2）當
，試判斷
的形狀，并說明理由；
（3）探究：當
______時，是等腰三角形．(請直接寫出答案)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某地方政府決定在相距50km的A、B兩站之間的公路旁E點，修建一個土特產加工基地，且使C、D兩村到E點的距離相等，已知DA⊥AB于A，CB⊥AB于B，DA=30km，CB=20km，那么基地E應建在離A站多少千米的地方？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，菱形ABCD中，已知∠BAD=120°，∠EGF=60°，∠EGF的頂點G在菱形對角線AC上運動，角的兩邊分別交邊BC，CD于點E，F．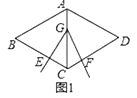
（1）如圖2，當頂點G運動到與點A重合時，求證：EC+CF=BC；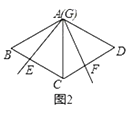
（2）知識探究：①如圖3，當頂點G運動到AC中點時，探究線段EC，CF與BC的數量關系；
②在頂點G的運動過程中，若 
=t，請直接寫出線段EC，CF與BC的數量關系（不需要寫出證明過程）；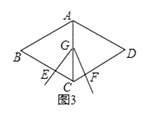
（3）問題解決：如圖4，已知菱形邊長為8，BG=7，CF= 
，當t＞2時，求EC的長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀與計算：請閱讀以下材料，并完成相應的任務．
斐波那契（約1170﹣1250）是意大利數學家，他研究了一列數，這列數非常奇妙，被稱為斐波那契數列（按照一定順序排列著的一列數稱為數列）．后來人們在研究它的過程中，發現了許多意想不到的結果，在實際生活中，很多花朵（如梅花、飛燕草、萬壽菊等）的瓣數恰是斐波那契數列中的數．斐波那契數列還有很多有趣的性質，在實際生活中也有廣泛的應用．斐波那契數列中的第n個數可以用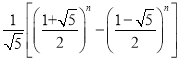
表示（其中，n≥1）．這是用無理數表示有理數的一個范例．
任務：請根據以上材料，通過計算求出斐波那契數列中的第1個數和第2個數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com