
【題目】如圖,D是△ABC的邊AB上一點,CN∥AB,DN交AC于點M,若MA=MC.
(1)求證:CD=AN ;
(2)若AC⊥DN,∠CAN=30°,MN=1,求四邊形ADCN的面積.
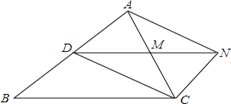
【答案】(1)證明:∵CN∥AB,∴∠DAC=∠NCA,即∠DAM=∠NCM。
在△AMD和△CMN中,∵∠DAM=∠NCM,MA="MC," ∠AMD∠CMN,
∴△AMD≌△CMN(ASA)。∴AD=CN,
又AD∥CN,∴四邊形ADCN是平行四邊形。
∴CD=AN。
(2)解:∵AC⊥DN,∠CAN=30°,MN=1,∴AN=2MN=2, 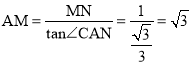 。
。
∴S△AMN![]() 。
。
∵四邊形ADCN是平行四邊形,
∴S四邊形ADCN=4S△AMN=2![]() 。
。
【解析】試題分析:(1)利用“平行四邊形ADCN的對邊相等”的性質可以證得CD=AN;
(2)根據銳角三角函數定義求得AN=2MN=2, AM=![]() ,則S四邊形ADCN=4S△AMN=2
,則S四邊形ADCN=4S△AMN=2![]() 。
。


 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南大學出版社系列答案
同步練習西南大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:初中數學 來源: 題型:
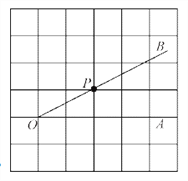
【題目】如圖,在![]() 的正方形網格中,點P是
的正方形網格中,點P是![]() 的邊OB上的一點.
的邊OB上的一點.
(1)過點P畫OB的垂線,交OA于點C;過點P畫OA的垂線,垂足為H;
(2)線段PH的長度是點P到直線__________的距離;
(3)線段__________的長度是點C到直線OB的距離;
(4)線段PC、PH、OC這三條線段大小關系是__________(用“<”號連接).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠A=30°,BC=2,將△ABC繞點C按順時針方向旋轉n度后,得到△EDC,此時點D在AB邊上,斜邊DE交AC于點F,則n=_______; 圖中陰影部分的面積為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在頻率分布直方圖中,以下說法錯誤的是( )
A.每個小長方形的面積等于頻數
B.每個小長方形的面積等于頻率
C.頻率=頻數÷數據總數
D.各個小長方形面積和等于1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,已知點P(2,1)與點Q(2,﹣1),下列描述正確是( )
A. 關于x軸對稱 B. 關于y軸對稱 C. 關于原點對稱 D. 都在y=2x的圖象上
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD的對角線相交于點O,AE平分∠BAD交BC于E,若∠CAE=15°,則∠AEO=( )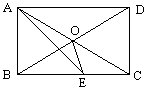
A.30°
B.25°
C.22.5°
D.20
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com