
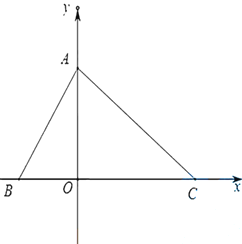
【題目】如圖在平面直角坐標系中,點![]() 、
、![]() 、
、![]() 且
且![]() ,
,
(1)求點![]() 、
、![]() 的坐標;
的坐標;
(2)求![]() 的面積
的面積![]() ;
;
(3)當點![]() 的坐標是
的坐標是![]() 且
且![]() 時,求
時,求![]() 的值.
的值.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根據平方和算術平方根的非負性求出a,b的值即可求出A、B的坐標;
(2)利用![]() ,即可求得;
,即可求得;
(3)分點P在y軸左邊時(上圖![]() 點),m <0及點P在y軸左邊時(上圖
點),m <0及點P在y軸左邊時(上圖![]() 點),m >0,列出方程求解即可.
點),m >0,列出方程求解即可.
解:(1)∵![]()
∴ ![]()
∴ ![]()
∴點A、 C的坐標分別為A(0,3)、C(4,0)。
(2)∵B(-2,0),
∴BC=4-(-2)=6
∴![]()
(3)∵P(m, 4),
∴點在直線y=4上,設直線y=4交軸于點D,連接BD,則D(0, 4), AD=4-3=1, PD= |m|.
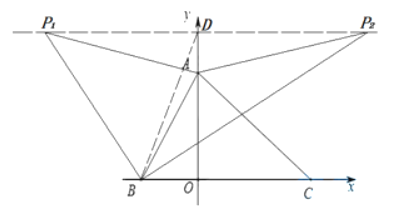
若點P在y軸左邊時(上圖![]() 點),m <0
點),m <0
∴![]()
∴![]()
即![]()
解得: m=![]()
若點P在y軸左邊時(上圖![]() 點),m >0
點),m >0
∴![]()
∴![]()
即![]()
解得: m=![]()
綜上所述:m的值為:![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=BC,D是BC上的一點,且滿足∠BAD= ![]() ∠C,以AD為直徑的⊙O與AB,AC分別相交于點E,F.
∠C,以AD為直徑的⊙O與AB,AC分別相交于點E,F.
(1)求證:直線BC是⊙O的切線;
(2)連接EF,若tan∠AEF= ![]() ,AD=4,求BD的長.
,AD=4,求BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
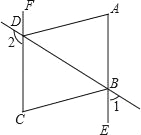
【題目】如圖,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE與FC會平行嗎?說明理由;
(2)AD與BC的位置關系如何?為什么?
(3)BC平分∠DBE嗎?為什么.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,點A、B、C在同一條直線上,點M為線段AC的中點、點N為線段BC的中點.
(1)如圖,當點C在線段AB上時:
①若線段![]() ,求
,求![]() 的長度.
的長度.
②若AB=a,求MN的長度.
(2)若![]() ,求MN的長度(用含
,求MN的長度(用含![]() 的代數式表示).
的代數式表示).
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,函數 y kx 與 y  的圖象交于 A、B 兩點,過 A 作 y 軸的垂線,交函數
的圖象交于 A、B 兩點,過 A 作 y 軸的垂線,交函數 的圖象于點 C,連接 BC,則△ABC 的面積為( )
的圖象于點 C,連接 BC,則△ABC 的面積為( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學知識伴隨著人類文明的起源而產生,人類祖先為我們留下了許多珍貴的原始資料,古巴比倫楔形文字泥板書就是其中之一,古巴比倫泥板上記載了兩種利用平方數表計算兩數乘積的公式:
![]() …①
…①
![]() …②
…②
(1)材料中,公式②中的空缺部分應該是 ;
(2)請你驗證材料中的公式①;
(3)當![]() ,
,![]() 時,利用公式①計算
時,利用公式①計算![]() 的值為 .
的值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形ABCD中,對角線AC,BD交于點O,點P在線段BC上(不含點B),∠BPE= ![]() ∠ACB,PE交BO于點E,過點B作BF⊥PE,垂足為F,交AC于點G.
∠ACB,PE交BO于點E,過點B作BF⊥PE,垂足為F,交AC于點G.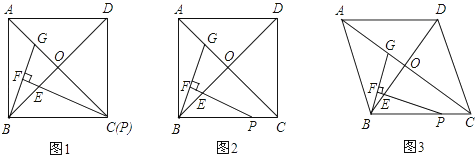
(1)當點P與點C重合時(如圖①),求證:△BOG≌△POE;
(2)結合圖②,通過觀察、測量、猜想: ![]() 與
與 ![]() 的關系,并證明你的猜想;
的關系,并證明你的猜想;
(3)把正方形ABCD改為菱形,其他條件不變(如圖③),若AC=8,BD=6,直接寫出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校九年級6個班舉行畢業文藝匯演,每班3個節目,有歌唱與舞蹈兩類節目,年級統計后發現歌唱類節目數比舞蹈類節目數的2倍少6個.設舞蹈類節目有![]() 個.
個.
(1)用含![]() 的代數式表示:歌唱類節目有______________個;
的代數式表示:歌唱類節目有______________個;
(2)求九年級表演的歌唱類與舞蹈類節目數各有多少個?
(3)該校七、八年級有小品節目參與匯演,在歌唱、舞蹈、小品三類節目中,每個節目的演出平均用時分別是5分鐘、6分鐘、8分鐘,預計全場節目交接所用的時間總共16分鐘.若從19:00開始,21:30之前演出結束,問參與的小品類節目最多能有多少個?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com