
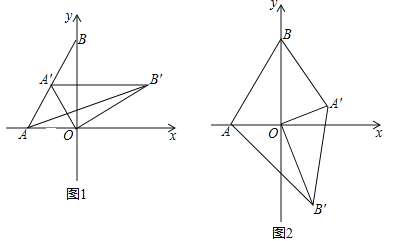
【題目】如圖1,在平面直角坐標系,O為坐標原點,點A(﹣1,0),點B(0,![]() ).
).
(1)求∠BAO的度數;
(2)如圖1,將△AOB繞點O順時針得△A′OB′,當A′恰好落在AB邊上時,設△AB′O的面積為S1,△BA′O的面積為S2,S1與S2有何關系?為什么?
(3)若將△AOB繞點O順時針旋轉到如圖2所示的位置,S1與S2的關系發生變化了嗎?證明你的判斷.
【答案】(1) ∠BAO=60°;(2) S1=S2;(3) S1=S2不發生變化;理由見解析.
【解析】
試題分析:(1)先求出OA,OB,再利用銳角三角函數即可得出結論;
(2)根據等邊三角形的性質可得AO=AA',再根據直角三角形30°角所對的直角邊等斜邊的一半求出AO=![]() AB,然后求出AO=AA’,,然后再根據等邊三角形的性質求出點O到AB的距離等于點A'到AO的距離,然后根據等底等高的三角形的面積相等解答;
AB,然后求出AO=AA’,,然后再根據等邊三角形的性質求出點O到AB的距離等于點A'到AO的距離,然后根據等底等高的三角形的面積相等解答;
(3)根據旋轉的性質可得BO=OB',AA'=OA',再求出∠AON=∠A'OM,然后再證明ΔAON≌ΔA'OM,可得AN=A'M,然后利用等底等高的三角形面積相等證明.
試題解析:(1)∵A(﹣1,0),B(0,![]() ),
),
∴OA=1,OB=![]() ,
,
在Rt△AOB中,tan∠BAO=![]() =
=![]() ,
,
∴∠BAO=60°;
(2)∵∠BAO=60°,∠AOB=90°,
∴∠ABO=30°,
∴CA'=AC=![]() AB,
AB,
∴OA'=AA'=AO,
根據等邊三角形的性質可得,△AOA'的邊AO、AA'上的高相等,
∴△BA'O的面積和△AB'O的面積相等(等底等高的三角形的面積相等),
即S1=S2.
(3)S1=S2不發生變化;
理由:如圖,過點'作A'M⊥OB.過點A作AN⊥OB'交B'O的延長線于N,
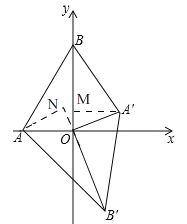
∵△A'B'O是由△ABO繞點O旋轉得到,
∴BO=OB',AO=OA',
∵∠AON+∠BON=90°,∠A'OM+∠BON=180°﹣90°=90°,
∴∠AON=∠A'OM,
在△AON和△A'OM中,
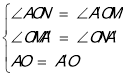 ,
,
∴△AON≌△A'OM(AAS),
∴AN=A'M,
∴△BOA'的面積和△AB'O的面積相等(等底等高的三角形的面積相等),
即S1=S2.


科目:初中數學 來源: 題型:
【題目】我們常用的數是十進制數,計算機程序使用的是二進制數(只有數碼0和1),它們兩者之間可以互相換算,如將(101)2,(1011)2換算成十進制數分別是(101)2=1×22+0×21+1=4+0+1=5,(1011)2=1×23+0×22+1×21+1=1l.按此方式,將二進制(10110)2換算成十進制數的結果是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有下列說法:
①有一個角為60°的等腰三角形是等邊三角形;
②三邊長為 ![]() 、
、 ![]() 、3的三角形為直角三角形;
、3的三角形為直角三角形;
③等腰三角形的兩邊長為3、4,則等腰三角形的周長為10;
④一邊上的中線等于這邊長的一半的三角形是等腰直角三角形.
其中正確的個數是( )
A.4個
B.3個
C.2個
D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=kx+b的圖象與反比例函數y=![]() 的圖象交于點A(﹣3,m+8),B(n,﹣6)兩點.
的圖象交于點A(﹣3,m+8),B(n,﹣6)兩點.
(1)求一次函數與反比例函數的解析式;
(2)求△AOB的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用![]() 紙復印文件,在甲復印店不管一次復印多少頁,每頁收費0.1元.在乙復印店復印同樣的文件,一次復印頁數不超過20時,每頁收費0.12元;一次復印頁數超過20時,超過部分每頁收費0.09元.
紙復印文件,在甲復印店不管一次復印多少頁,每頁收費0.1元.在乙復印店復印同樣的文件,一次復印頁數不超過20時,每頁收費0.12元;一次復印頁數超過20時,超過部分每頁收費0.09元.
設在同一家復印店一次復印文件的頁數為![]() (
(![]() 為非負整數).
為非負整數).
(1)根據題意,填寫下表:
一次復印頁數(頁) | 5 | 10 | 20 | 30 | … |
甲復印店收費(元) |
| 2 | … | ||
乙復印店收費(元) |
|
| … |
(2)設在甲復印店復印收費![]() 元,在乙復印店復印收費
元,在乙復印店復印收費![]() 元,分別寫出
元,分別寫出![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(3)當![]() 時,顧客在哪家復印店復印花費少?請說明理由.
時,顧客在哪家復印店復印花費少?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AOB=30°,∠AOB內有一定點P,且OP=10.在OA上有一點Q,OB上有一點R.若△PQR周長最小,則最小周長是( )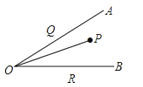
A.10
B.15
C.20
D.30
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,坐標平面上,△ABC≌△DEF全等,其中A、B、C的對應頂點分別為D、E、F,且AB=BC,若A、B、C的坐標分別為(﹣3,1)、(﹣6,﹣3)、(﹣1,﹣3),D、E兩點在y軸上,則F點到y軸的距離為 . 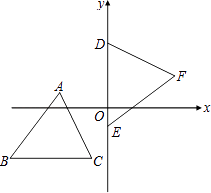
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com